Question

Wheel is in pure rolling find speed. of point B, it speed of A is 8 m/s

$V_A = 8$ B

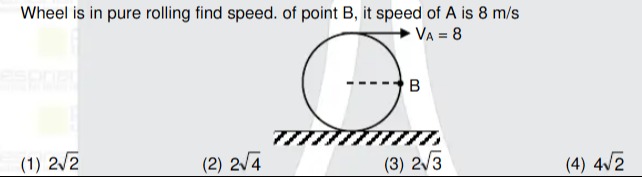
• A. $2\sqrt{2}$
• B. $2\sqrt{4}$
• C. $2\sqrt{3}$
• D. $4\sqrt{2}$

Answer 1

Answer: (D)

$4\sqrt{2} \, \text{m/s}$

Answer 2

1. In pure rolling, the center speed is $v$ and the wheel's angular speed is $\omega = \frac{v}{R}$.

2. The top point (A) has speed:

   $$V_A = v + \omega R = v + v = 2v.$$

3. Given $V_A = 8 \, \text{m/s}$, we have $2v = 8$ so $v = 4 \, \text{m/s}$.

4. For point B (at the rightmost point), its velocity is the vector sum of the center speed $v$ (horizontal rightward) and the rotational contribution $\omega R = 4 \, \text{m/s}$ (vertical upward, due to clockwise rotation).

5. Thus, the speed of B is:

   $$V_B = \sqrt{4^2 + 4^2} = \sqrt{16 + 16} = \sqrt{32} = 4\sqrt{2} \, \text{m/s}.$$