Question

What would be the voltage across ${{C}_{3}}$?

A. $\dfrac{\left( {{C}_{1}}+{{C}_{2}} \right)V}{{{C}_{1}}+{{C}_{2}}+{{C}_{3}}}$
B.$\dfrac{{{C}_{1}}V}{{{C}_{1}}+{{C}_{2}}+{{C}_{3}}}$
C. $\dfrac{{{C}_{2}}V}{{{C}_{1}}+{{C}_{2}}+{{C}_{3}}}$
D. $\dfrac{{{C}_{3}}V}{{{C}_{1}}+{{C}_{2}}+{{C}_{3}}}$

Answer 1

As a first step, you could find the effective capacitance of all the three capacitors connected in the circuit. Then, you could recall the expression for the relation between the voltage, capacitance and charge. Then you could use this expression and substitute accordingly to find the voltage across ${{C}_{3}}$.

Formula used:
Effective capacitance:
For capacitors in series,
$C={{C}_{a}}+{{C}_{b}}$
For capacitors in parallel,
$\dfrac{1}{C}=\dfrac{1}{{{C}_{a}}}+\dfrac{1}{{{C}_{b}}}$

Complete Step by step solution:
In the question, we are given a circuit that contains 3 capacitors and a voltage source.

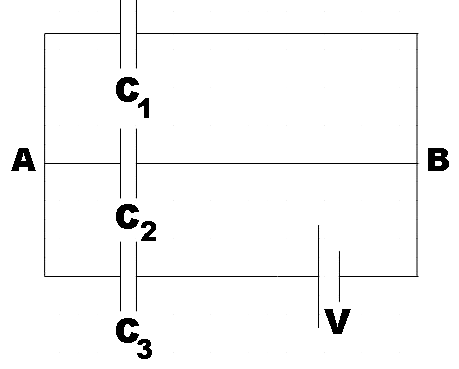
From the figure, we see that the capacitance across the terminals A and B will be the effective capacitance of the two capacitors${{C}_{1}}$ and ${{C}_{2}}$ connected in parallel.

We know that the capacitance of two capacitors in parallel is given by,
$C={{C}_{a}}+{{C}_{b}}$

Therefore, we find that,
${{C}_{AB}}={{C}_{1}}+{{C}_{2}}$

Now we see that this capacitor would be series with the remaining capacitor${{C}_{3}}$. We know that the effective capacitance of two capacitors connected in series would be,
$\dfrac{1}{C}=\dfrac{1}{{{C}_{a}}}+\dfrac{1}{{{C}_{b}}}$

So the effective capacitance would be,
${{C}_{eff}}=\dfrac{{{C}_{3}}\times {{C}_{AB}}}{{{C}_{3}}+{{C}_{AB}}}$
$\Rightarrow {{C}_{eff}}=\dfrac{{{C}_{3}}\left( {{C}_{1}}+{{C}_{2}} \right)}{{{C}_{1}}+{{C}_{2}}+{{C}_{3}}}$

Now let us recall the expression between voltage, capacitance and charge which is given by,
$Q=CV$

So the charge on the capacitor ${{C}_{3}}$ would be,
$Q={{C}_{eff}}V=\dfrac{{{C}_{3}}\left( {{C}_{1}}+{{C}_{2}} \right)}{{{C}_{1}}+{{C}_{2}}+{{C}_{3}}}V$

Now the voltage across the capacitor ${{C}_{3}}$ would be,
${{V}_{3}}=\dfrac{Q}{{{C}_{3}}}$
$\therefore {{V}_{3}}=\dfrac{\left( {{C}_{1}}+{{C}_{2}} \right)V}{{{C}_{1}}+{{C}_{2}}+{{C}_{3}}}$

Therefore, we found the voltage across the capacitor ${{C}_{3}}$ to be,
${{V}_{3}}=\dfrac{\left( {{C}_{1}}+{{C}_{2}} \right)V}{{{C}_{1}}+{{C}_{2}}+{{C}_{3}}}$

Hence, option A is found to be the correct answer.

Note:
Finding equivalent capacitance in a circuit can be done by simply considering the circuit part by part. Thus, we would be able to break the complex combination into simple series and parallel connections. Here in the given circuit, we found two capacitors connected in parallel to which a third capacitor is in series.