Question

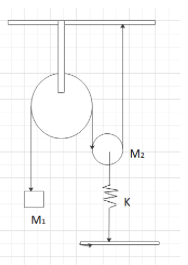
What would be the period of the free oscillations of the system shown here if mass ${M_1}$ is pulled down a little? Force constant of the spring is$k$, the mass of fixed pulley is negligible and movable pulley is smooth

A)$T = 2\pi \sqrt {\dfrac{{{M_1} + {M_2}}}{k}}$
B)$T = 2\pi \sqrt {\dfrac{{{M_1} + 4{M_2}}}{k}}$
C) $T = 2\pi \sqrt {\dfrac{{{M_2} + 4{M_1}}}{k}}$
D)$T = 2\pi \sqrt {\dfrac{{{M_2} + 3{M_1}}}{k}}$

Answer 1

In this question, we can calculate the force equations for both masses. After that we can use both equations and deduce them in one equation. We have to simplify the equation to form the equation of SHM. After comparing this equation with the standard equation, we can find the expression for frequency.

Complete step by step solution: -
Let the system spring extended by $x$at equilibrium position. Then in this position the tension of mass ${M_1}$is ${T'}$and mass ${M_2}$(pulley) be $2{T'}$.
So, we have force equation as for the both masses-
For${M_1}$, $T = {M_1}g$
And for${M_2}$, $k{x_0} = 2T - {M_2}g$.................(i)
Now consider displacement of mass ${M_2}$displaced by$x$. The corresponding displacement for mass of block ${M_1}$is$2x$. And in this position tension on ${M_1}$be ${T^{''}}$ and on ${M_2}$be $2{T^{''}}$.
So, for${M_2}$,
${M_2}\dfrac{{{d^2}x}}{{d{t^2}}} = 2{T^{''}} - {M_2}g - kx - k{x_0}$................(ii)
For ${M_1}$
${M_1}\dfrac{{{d^2}(2x)}}{{d{t^2}}} = {M_1}g - {T^{''}}$.........................(iii)
Multiplying equation (iii) by $2$and adding it with equation (ii), we get
$({M_2} + 4{M_1})\dfrac{{{d^2}x}}{{d{t^2}}} = 2{M_1}g - {M_2}g - kx - k{x_0}$
Putting the value of$k{x_0}$, we get-

$$({M_2} + 4{M_1})\dfrac{{{d^2}x}}{{d{t^2}}} = 2{M_1}g - {M_2}g - kx - 2{M_1}g + {M_2}g \\\ \Rightarrow ({M_2} + 4{M_1})\dfrac{{{d^2}x}}{{d{t^2}}} = - kx \\\$$ $$\Rightarrow \dfrac{{{d^2}x}}{{d{t^2}}} + \dfrac{{kx}}{{({M_2} + 4{M_1})}} = 0 \\\ \Rightarrow \dfrac{{{d^2}x}}{{d{t^2}}} + \left( {\dfrac{k}{{({M_2} + 4{M_1})}}} \right)x = 0 \\\$$

Comparing this equation with $\dfrac{{{d^2}x}}{{d{t^2}}} + \omega x = 0$, we get-
Angular frequency, $\omega = \sqrt {\dfrac{k}{{{M_2} + 4{M_1}}}}$
We know that the time period, $T = \dfrac{{2\pi }}{\omega }$
Putting the value of$\omega$, we get-

$$T = \dfrac{{2\pi }}{{\sqrt {\dfrac{k}{{{M_2} + 4{M_1}}}} }} \\\ \Rightarrow T = 2\pi \sqrt {\dfrac{{{M_2} + 4{M_1}}}{k}} \\\$$

Therefore, option C is correct.

Note: - In this question, we have to remember that the force equations for both masses are different for the first mass there is no spring so the equation does not have a spring constant. While for the second mass the spring is attached so the spring constant part will be in the equation. We have to try to deduce the equation in such a way that the final equation will be in the form of $\dfrac{{{d^2}x}}{{d{t^2}}} + \omega x = 0$.