Question

What will be the work done in shifting a charge from a point X to a point Y in the diagram as shown in figure?

A. $\dfrac{5\left( \sqrt{5}-1 \right)K{{q}^{2}}}{d\sqrt{5}}$
B. $\dfrac{4\left( \sqrt{5}-1 \right)K{{q}^{2}}}{d\sqrt{5}}$
C. $\dfrac{6\left( \sqrt{5}-1 \right)K{{q}^{2}}}{d\sqrt{5}}$
D. $\dfrac{\left( \sqrt{5}-1 \right)K{{q}^{2}}}{d\sqrt{5}}$

Answer 1

Work done to move a unit charge from one point to another is the change in potential between those points. To determine the work done, we first need to determine potential at point X and point Y due to system of charges. Then, we can calculate work to be done by multiplying the magnitude of charge moved to the difference in potential between those points.

Complete answer:
Electric potential at a point is defined as work done to move a unit positive charge from infinity to that point in an electric field without accelerating.
Electric potential in free space at a point at distance $r$ from a single charge $q$ is given by
$V=\dfrac{q}{4\pi {{\epsilon }_{0}}r}$
Potential is a scalar quantity. So for a system of charges, net potential at a point is the sum of potential due to each charge.

Let us mark the positions of charge as A,B,C and D as shown in figure.

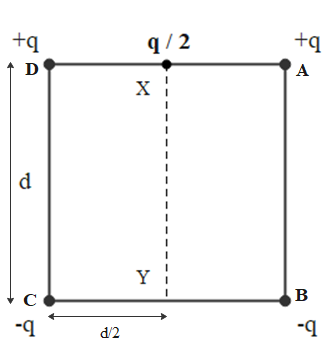
Potential at point X due to system of charges is
${{V}_{X}}={{V}_{XA}}+{{V}_{XB}}+{{V}_{XC}}+{{V}_{XD}}$
${{V}_{X}}=\dfrac{q}{4\pi {{\epsilon }_{0}}(AX)}+\dfrac{-q}{4\pi {{\epsilon }_{0}}(BX)}+\dfrac{-q}{4\pi {{\epsilon }_{0}}(CX)}+\dfrac{q}{4\pi {{\epsilon }_{0}}(DX)}$
${{V}_{X}}=\dfrac{q}{4\pi {{\epsilon }_{0}}}\left( \dfrac{1}{(d/2)}+\dfrac{-1}{(\sqrt{5}d/2)}+\dfrac{-1}{(\sqrt{5}d/2)}+\dfrac{1}{(d/2)} \right)=\dfrac{q}{4\pi {{\epsilon }_{0}}}\left( \dfrac{4}{d}-\dfrac{4}{\sqrt{5}d} \right)$
${{V}_{X}}=\dfrac{q}{4\pi {{\epsilon }_{0}}d}\left( \dfrac{4(\sqrt{5}-1)}{\sqrt{5}} \right)$
Similarly, potential at Y due to this system of charges is
${{V}_{Y}}=\dfrac{-q}{4\pi {{\epsilon }_{0}}d}\left( \dfrac{4(\sqrt{5}-1)}{\sqrt{5}} \right)$
The change in potential when charge is moved to point Y
$\Delta V={{V}_{X}}-{{V}_{Y}}=\dfrac{q}{4\pi {{\epsilon }_{0}}d}\left( \dfrac{4(\sqrt{5}-1)}{\sqrt{5}} \right)-\dfrac{-q}{4\pi {{\epsilon }_{0}}d}\left( \dfrac{4(\sqrt{5}-1)}{\sqrt{5}} \right)$
$\Rightarrow \Delta V=\dfrac{2q}{\pi {{\epsilon }_{0}}d}\left( \dfrac{(\sqrt{5}-1)}{\sqrt{5}} \right)$
This is the work done in moving a unit positive charge from X to Y. When charge of magnitude $q/2$ is moved, work done
$W=\dfrac{q}{2}\Delta V=\dfrac{{{q}^{2}}}{\pi {{\epsilon }_{0}}d}\left( \dfrac{(\sqrt{5}-1)}{\sqrt{5}} \right)=\dfrac{K{{q}^{2}}}{d}\left( \dfrac{4(\sqrt{5}-1)}{\sqrt{5}} \right)$
Here $K=\dfrac{1}{4\pi {{\epsilon }_{0}}}$

So, the correct answer is “Option D”.

Note:
If the charge is situated in a medium of permittivity $\epsilon$ then the magnitude of potential due to charge will be, $V=\dfrac{q}{4\pi \epsilon r}$
Potential is a scalar quantity. So for a system of charges, net potential at a point is the sum of potential due to each charge.