Question

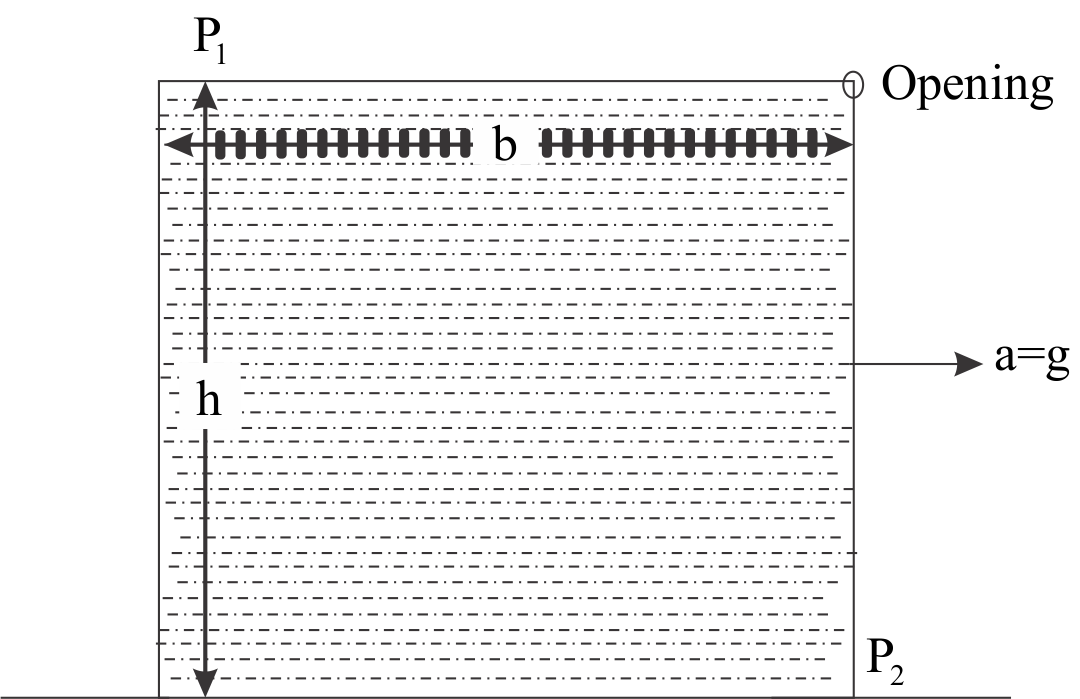
What will be the value of pressure difference $\left( {{P_1} - {P_2}} \right)$ if the closed rectangular vessel is completely filled with the liquid of density $\rho$ which moves with the acceleration of $a = g$?

(A) $\rho gb$
(B) $\dfrac{{\rho g\left( {b + h} \right)}}{2}$
(C) $\rho \left( {ab - gh} \right)$
(D) $\rho gh$

Answer 1

Acceleration has no effect on pressure. Find the pressure for vertical direction for the rectangular vessel and then, find the pressure for horizontal direction then, using both the equations of pressure find their difference.

Complete step by step solution:
Barometer is the instrument which is used to measure atmospheric pressure which is especially used for forecasting the weather and determines the altitude and a manometer is the device which uses the column of liquid to measure pressure.
First of all, we have to find the pressure for vertical direction.
According to the question, it is given that, density of liquid is $\rho$ and the acceleration is $a = g$
So, as we know that, force can be defined as the product of mass and acceleration –
$\therefore F = ma$
So, in the question, $a = g$ and $m = \rho hA$
So, pseudo force is equal to, $F = \rho hAg$
Now, finding the pseudo pressure –
$\therefore {P_{pseudo}} = \dfrac{F}{A}$
Putting the value of force in the above formula –
$\Rightarrow {P_{pseudo}} = \dfrac{{\rho hAg}}{A} \\\ \Rightarrow {P_{pseudo}} = \rho gh \\\$

$${P_2} = {P_1} + {P_{pseudo}} \\\ \Rightarrow {P_2} - {P_1} = {P_{pseudo}} \\\ \therefore {P_2} - {P_1} = \rho gh \cdots \left( 1 \right) \\\$$

Now, calculating the pressure for the horizontal direction
${P_2} + \rho ab = {P_1} \\\ \Rightarrow {P_2} - {P_1} = \rho ab \cdots \left( 2 \right) \\\$
The pressure has only magnitude and no direction is associated with it therefore, the pressure is the scalar quantity. Hence, from equation $\left( 1 \right)$ and $\left( 2 \right)$, we get –
$\Rightarrow {P_2} - {P_1} = \rho \left( {ab - gh} \right)$
Hence, the pressure difference is $\rho \left( {ab - gh} \right)$.

Therefore, the correct option is (C).

Note: The formula of pressure, $P = \rho gh$ is useful for the situations when the density and acceleration due to gravity are the functions of height. This is the hydrostatic pressure in the liquid.