Question

What will be the reaction between hinge and rod at point A?

$\left( a \right)\sqrt{65}\dfrac{Mg}{4}$
$\left( b \right)2Mg$
$\left( c \right)\sqrt{17}\dfrac{Mg}{4}$
$\left( d \right)\sqrt{17}\dfrac{Mg}{2}$

Answer 1

There are two rods connected to the fringe and clearly these are at equilibrium, so, we will find all the forces due to gravity as well as due to tension. After this we will put at equal the two horizontal as well as vertical forces.
Formula used:
${{F}_{hor.}}=T,{{F}_{ver.}}=2Mg,{{F}_{hor.}}={{F}_{ver.}}$ where T is tension, M is mass and g is force due to gravity, $F=\sqrt{{{\left( {{F}_{hor.}} \right)}^{2}}+{{\left( {{F}_{ver.}} \right)}^{2}}}$.

Complete answer:
Hinge: It is a connector which connects two different objects together. It is made up of metal also, that is we will find it mostly used in our doors and many big boxes.
Now, we will look for the forces that are acting on the rod and the hinge. This can be understood by the help of a diagram as shown below.

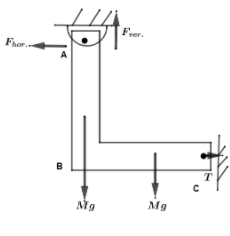
From this figure we come to know that there are two horizontal forces acting on the rods but they are not opposite to each other. So, suppose that the horizontal force that is acting on A is denoted by ${{F}_{hor.}}$. Also, the horizontal force that is acting is on the point A. This is just a tension that has been created at this point. So, by being as horizontal forces they are going to be equal. Thus, we get ${{F}_{hor.}}=T$…(i).
Now, we will also notice the forces that are acting as a vertical force. This is represented by ${{F}_{ver.}}$ which is acting on A. If we get precise then this force is acting on the rod AB. Also, we will notice that the force acting on the rod BC is due to gravity. Due to gravity we get that the forces acting on these two rods are Mg only.
This means that the total vertical force will be ${{F}_{ver.}}=2Mg$…(ii). As, the vertical force is clearly twice the horizontal force and since, this is in equilibrium so; the vertical as well as the horizontal forces will be equal. Therefore, we have
$\begin{aligned} & {{F}_{hor.}}={{F}_{ver.}} \\\ & \Rightarrow 2T=Mg \\\ & \Rightarrow T=\dfrac{Mg}{2} \\\ \end{aligned}$
Now, we will find the magnitude of both the forces. So, we get that ${{F}_{hor.}}=T=\dfrac{Mg}{2}$…(iii). The total force after this will be the sum of magnitudes of horizontal and vertical forces. Thus,

& F=\sqrt{{{\left( {{F}_{hor.}} \right)}^{2}}+{{\left( {{F}_{ver.}} \right)}^{2}}} \\\ & \Rightarrow F=\sqrt{{{\left( \dfrac{Mg}{2} \right)}^{2}}+{{\left( 2Mg \right)}^{2}}} \\\ & \Rightarrow F=\sqrt{\dfrac{{{M}^{2}}{{g}^{2}}}{4}+4{{M}^{2}}{{g}^{2}}} \\\ & \Rightarrow F=Mg\sqrt{\dfrac{1}{4}+4} \\\ & \Rightarrow F=Mg\sqrt{\dfrac{1+16}{4}} \\\ & \Rightarrow F=Mg\sqrt{\dfrac{17}{4}} \\\ & \Rightarrow F=\dfrac{\sqrt{17}}{2}Mg \\\ \end{aligned}$$ **So, the correct option is $\left( d \right)\sqrt{17}\dfrac{Mg}{2}$ .** **Note:** To solve such types of questions, it is important to find all forces that are acting towards it. By all the forces we mean most importantly forces due to gravitation and the force due to tension created at any point. Here, the question does not mention the equilibrium but we come to know that it is in equilibrium because it does not tilt or does not get shifted to any other position. The magnitude of horizontal and vertical gives the total force because the horizontal and vertical are just the components of the force.