Question

What will be the potential difference ${{V}_{B}}-{{V}_{A}}$ in the network given below?

& A.7V \\\ & B.6V \\\ & C.5V \\\ & D.8V \\\ \end{aligned}$$

Answer 1

First of all we have to formulate the equivalent resistances in both the branches in A and B. The resistors which are connected in series will be having an equivalent resistance equal to the sum of the resistances of individual resistors. Find the ratio of the equivalent voltage to the equivalent resistance. Substitute the values in it and find the answers. This will help you in answering this question.

Complete answer:
First of all we have to formulate the equivalent resistances in both the branches in A and B. Therefore we can draw it like this.

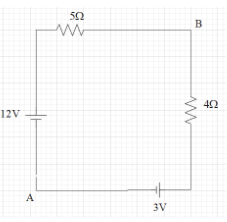
The resistors which are connected in series will be having an equivalent resistance equal to the sum of the resistances of individual resistors.
Therefore the ratio of the equivalent voltage to the equivalent resistance can be written as,
$\dfrac{{{E}_{eq}}}{{{r}_{eq}}}=\dfrac{{{E}_{1}}}{{{r}_{1}}}+\dfrac{{{E}_{2}}}{{{r}_{2}}}$
Substituting the values in it will give,
$\dfrac{{{E}_{eq}}}{{{r}_{eq}}}=\dfrac{12}{5}+\dfrac{3}{4}=\dfrac{63}{20}$
The equivalent resistance can be found by the analysis of the circuit. Here we can see that the resistances are parallel. Therefore their equivalent resistance can be found by the equation,
$\dfrac{1}{{{r}_{eq}}}=\dfrac{1}{{{r}_{1}}}+\dfrac{1}{{{r}_{2}}}$
Substituting the values in the equation will give,
$\begin{aligned} & \dfrac{1}{{{r}_{eq}}}=\dfrac{1}{4}+\dfrac{1}{5} \\\ & \Rightarrow {{r}_{eq}}=\dfrac{4\times 5}{9}=\dfrac{20}{9}\Omega \\\ \end{aligned}$
As we already mentioned, the ratio of the equivalent voltage to the equivalent resistance is given as,
$\dfrac{{{E}_{eq}}}{{{r}_{eq}}}=\dfrac{63}{20}$
Let us rearrange this equation as,
${{E}_{eq}}=\dfrac{63}{20}\times {{r}_{eq}}$
Substituting the values in it will give,
${{E}_{eq}}=\dfrac{63}{20}\times \dfrac{20}{9}=7V$
Therefore the circuit can be redrawn as,

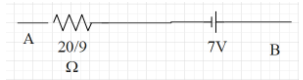
Hence the potential difference between the point A and B is found to be $7V$.

This has been mentioned as option A.

Note:
If the resistance are connected in series, then their equivalent resistance can be found by taking the sum of the individual resistances. If the resistances are connected in parallel then the reciprocal of the equivalent resistance can be found by taking the sum of the reciprocal of the individual resistances.