Question

What will be the net resistance between A and B:

A. $\dfrac{3}{2} (\sqrt{5} - 1) \Omega$
B. $\dfrac{3}{2} (\sqrt{5} + 1) \Omega$
C. $\dfrac{3\sqrt{5}}{2} \Omega$
D. 3 $\Omega$

Answer 1

Assume the resistance of the entire series to be x, which means x is the equivalent resistance of the entire series. Then, take a small part of the repeating infinite series and add it to x. This addition should again give x.
Formula used:
For two resistances A and B in a parallel network, the equivalent resistance is given by:
$\dfrac{1}{R} = \dfrac{1}{A} + \dfrac{1}{B}$.

Complete answer:
Consider the following circuit first, where we have taken the resistance of the entire series to be x.

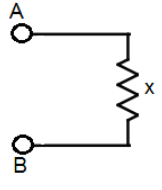
Now, we add an element of the infinite series to create the following network across PQ.

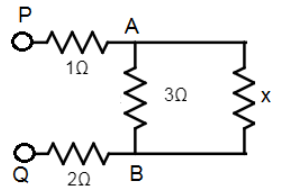
Now, across point AB, we have a resistance given by:
$\dfrac{1}{R_{AB}} = \dfrac{1}{x} + \dfrac{1}{3}$.
We write this because, two resistances x and 3 ohms are forming a parallel network. So the equivalent resistance will be a result of parallel combination.
Simplification of the preceding equation gives:
$R_{AB} = \dfrac{3x}{x+3}$.
Now, across the points P and Q, we can determine the total resistance as:
$R_{PQ} = 1 \Omega + R_{AB} + 2 \Omega = 3 \Omega + R_{AB}$.
Here, across AB, we made an equivalent resistance $R_{AB}$ replacement and the remaining two can be observed to be in series to this resistance.
But, consider the fact that after adding the repeating unit, we still have the same infinite series (after all it’s infinite). Therefore, the resistance across PQ is still x only.
So, we can write this in the preceding equation as:
$x = 3 + \dfrac{3x}{x+3}$.
Here, we did not mind to put units in place and we also made the substitution for $R_{AB}$ along with $R_{PQ}$.
With the help of preceding equation, we are now able to write a quadratic equation of the form,
$x^2 – 3x -9 = 0$.
This equation produces two roots,
$\dfrac{3}{2} ( 1 + \sqrt{5})$ and $\dfrac{3}{2} ( 1 - \sqrt{5})$.
We discard the one with the negative sign, as it is clearly visible that it produces negative resistance value.
The value of resistance for the entire series across AB is $\dfrac{3}{2} (\sqrt{5} + 1) \Omega$.

Therefore, the correct answer that we are able to observe for here is option (B).

Note:
For a beginner, to observe parallel circuits in big networks becomes challenging. In a parallel combination, two resistances are always connected by their two endpoints. While in a series network, resistances are always connected keeping only one end point in common.