Question

What will be the locus at equal distance from two parallel lines in a plane?

Answer 1

We will consider two parallel lines and first we will write their equations. Now we will find the distance of the given point from the first line and then distance of the point from the second line. Since, the point is equidistant from both the parallel lines we will equate the distance of point from first line to the distance of point from the second line. Solving this equation will give the locus of the point equidistant from two parallel lines.

Complete answer:

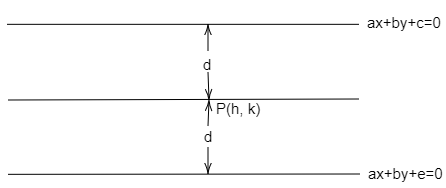
Let us consider two parallel lines $ax + by + c = 0$ and $ax + by + e = 0$ .
Also, let the point which is at equal distance from two parallel lines be $P(h,k)$ .
Distance ($d$) of a point $({x_1},{y_1})$ from a line $lx + my + n = 0$ is given by $d = \dfrac{{\left| {l{x_1} + m{y_1} + n} \right|}}{{\sqrt {{l^2} + {m^2}} }}$ .
Therefore, Distance of $P(h,k)$ from the line $ax + by + c = 0$ is
$\Rightarrow d = \dfrac{{\left| {ah + bk + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} - - - (1)$
Similarly, Distance of $P(h,k)$ from the line $ax + by + e = 0$ is
$\Rightarrow d = \dfrac{{\left| {ah + bk + e} \right|}}{{\sqrt {{a^2} + {b^2}} }} - - - (2)$
From $(1)$ and $(2)$ we get
$\Rightarrow \dfrac{{\left| {ah + bk + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \dfrac{{\left| {ah + bk + e} \right|}}{{\sqrt {{a^2} + {b^2}} }}$
Squaring both the sides, we get
$\Rightarrow \dfrac{{{{\left| {ah + bk + c} \right|}^2}}}{{{a^2} + {b^2}}} = \dfrac{{{{\left| {ah + bk + e} \right|}^2}}}{{{a^2} + {b^2}}}$
On eliminating ${a^2} + {b^2}$ from the denominator of both the sides, we get
$\Rightarrow {\left| {ah + bk + c} \right|^2} = {\left| {ah + bk + e} \right|^2}$
As ${\left| r \right|^2} = {r^2}$ for all $r \in R$ .
Therefore, we get
$\Rightarrow {\left( {ah + bk + c} \right)^2} = {\left( {ah + bk + e} \right)^2}$
On simplification we get,
$\Rightarrow {a^2}{h^2} + {b^2}{k^2} + {c^2} + 2abhk + 2bck + 2ach = {a^2}{h^2} + {b^2}{k^2} + {e^2} + 2abhk + 2bek + 2aeh$
Taking all the terms of R.H.S. to L.H.S.
$\Rightarrow {a^2}{h^2} + {b^2}{k^2} + {c^2} + 2abhk + 2bck + 2ach - {a^2}{h^2} - {b^2}{k^2} - {e^2} - 2abhk - 2bek - 2aeh = 0$
On simplifying,
$\Rightarrow 2ach - 2aeh + 2bck - 2bek + {c^2} - {e^2} = 0$
Taking $2ah$ common from first two terms and $2bk$ common from third and fourth term,
$\Rightarrow 2a\left( {c - e} \right)h + 2b\left( {c - e} \right)k + \left( {{c^2} - {e^2}} \right) = 0$
On rewriting the equation,
$\Rightarrow 2a\left( {c - e} \right)h + 2b\left( {c - e} \right)k + \left( {c - e} \right)\left( {c + e} \right) = 0$
Taking $\left( {c - e} \right)$ common,
$\Rightarrow \left( {c - e} \right)\left( {2ah + 2bk + c + e} \right) = 0$
On equating we get
$\Rightarrow \left( {c - e} \right) = 0$ or $\left( {2ah + 2bk + c + e} \right) = 0$
But, if $c = e$ both lines will coincide. Therefore, $c \ne e$ .
Now, when $\left( {2ah + 2bk + c + e} \right) = 0$
Taking $2$ common, we get
$\Rightarrow ah + bk + \dfrac{{c + e}}{2} = 0$
Replacing $(h,k)$ with $(x,y)$ we get,
$\Rightarrow ax + by + \dfrac{{c + e}}{2} = 0$
Hence, the locus of a point at equal distance from two parallel lines in a plane is a straight line parallel to both the given lines.

Note:
Since, it is given that the lines are parallel that’s why we can consider the equation of lines as $ax + by + c = 0$ and $ax + by + e = 0$ because parallel lines have equal slopes and as we know that ${\text{Slope of a line}} = - \dfrac{{{\text{coefficient of x}}}}{{{\text{coefficient of y}}}}$ . Therefore, in this case both the lines have slope $\left( { - \dfrac{a}{b}} \right)$ . But in other cases when lines are not parallel, we cannot take these equations for two lines as non-parallel lines have different slopes.