Solveeit Logo
Login

Question

Question: What will be the height of the image when an object of 2 mm is placed at a distance 20 cm in front o...

What will be the height of the image when an object of 2 mm is placed at a distance 20 cm in front of the axis of a convex mirror of radius of curvature 40 cm?
A. 20 mm
B. 10 mm
C. 6 mm
D. 1 mm

Explanation

Solution

Magnification is the increase in size of image as compared to the object when placed in front of an optical system.
First determine the distance of the image from the pole using the mirror formula and then use the magnification formula to determine the height of the image.

Formula used: Magnification, m=−vum=-\dfrac{v}{u} and mirror formula, 1f=1v+1u\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}

Complete step by step answer:
The object is placed at a distance 20 cm from the pole of the mirror. The distance of object is always taken negative i.e. u=20 cmu=20\,cm

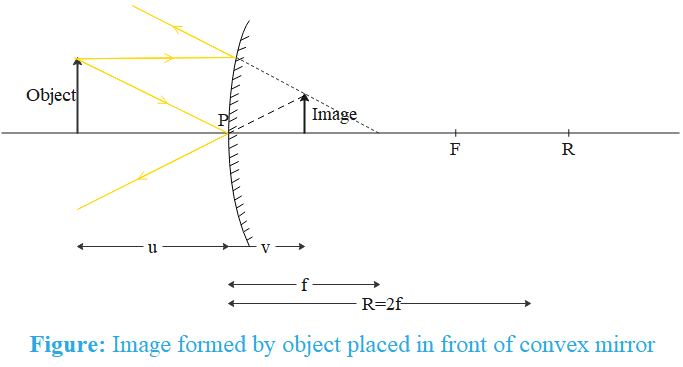
The focus of the convex mirror lies in the direction of incident light from the pole therefore, the focal length of the convex mirror is positive. Also focal length of a mirror is half of its radius of curvature i.e. f=R2=−20 cmf=\dfrac{R}{2}=-20\,cm
Now, we use mirror formula
120=1v+1−20⇒1v=120+120=110\dfrac{1}{20}=\dfrac{1}{v}+\dfrac{1}{-20}\Rightarrow \dfrac{1}{v}=\dfrac{1}{20}+\dfrac{1}{20}=\dfrac{1}{10}
⇒v=10cm\Rightarrow v=10cm
Since the image distance is positive, the image is behind the mirror, so the image is virtual and upright.
Magnification is the ratio of height of image (h’) to height of object (h).
m=−vu=h′hm=\dfrac{-v}{u}=\dfrac{h'}{h}
Height of the object is h=2mmh=2mm
Substituting the values, we get
−10cm−20cm=0.5=h′2mm-\dfrac{10cm}{-20cm}=0.5=\dfrac{h'}{2mm}
⇒h′=0.5×2mm=1mm\Rightarrow h'=0.5\times 2mm=1mm

So, the correct answer is “Option D”.

Additional Information: By sign convention, the object is always placed towards the left from the pole. Therefore, its distance from the pole is always negative.
All distances are measured from the pole of the mirror. Distances measured in the direction of the incident light are positive and the distances measured in the direction opposite to that are negative.

Note: In mirror as well as optical lens problems, the most important thing to consider is sign conventions. Therefore, students should understand the sign conventions properly and then proceed with the solution. Diagrams are very helpful in understanding the sign conventions.
The distances in the direction of incident light from the pole are taken positively.