Question

What will be the efficiency of the cycle as shown in the figure?
$1\to 2~$ and $4\to 5~$ are adiabatic process;
$3\to 4~$ and $5\to 1~$ are, isobaric process,
$2\to 3~$ is isochoric process ${{Q}_{23}}=10~J,{{Q}_{34}}=15~J~$ and ${{Q}_{51}}=-10~J.$

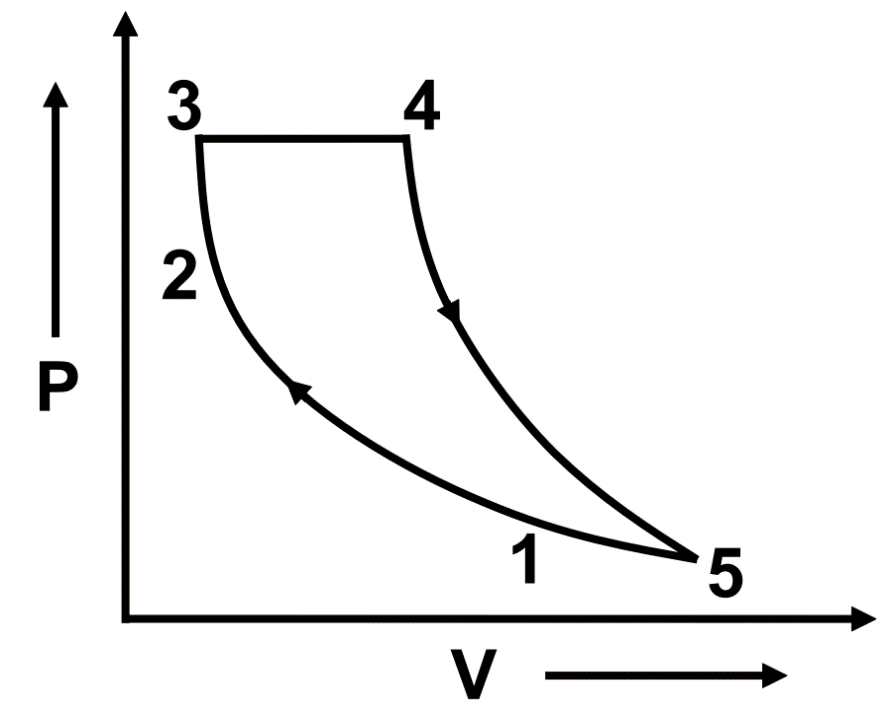
(A) $45$
(B) $100$
(C) $60$
(D) None of these.

Answer 1

We know that there are four thermodynamics processes: isobaric, isochoric, isothermal, and adiabatic. In isothermal processes temperature remains constant, in adiabatic processes there is no transfer of heat, also in isochoric processes volume remains constant and isobaric process pressure remains constant.

Complete answer:
As we know from the Carnot theorem, the reversible engine will always have a greater efficiency than the irreversible one. Efficiency signifies a peak level of performance that uses the least amount of inputs to achieve the highest amount of output. Efficiency requires reducing the number of unnecessary resources used to produce a given output including personal time and energy. The reversible heat engine operates on a reverse cycle and functions as a heat pump/refrigerator. The Carnot cycle is reversible representing the upper limit on the efficiency of an engine cycle. Also, in Physics, when the system gas does work i.e. it loses energy it is taken as positive and when work is done on the gas i.e. it gains energy it is taken as negative.
$\eta =\dfrac{{{W}_{net}}}{\Delta {{Q}_{supplied}}}\times 100$ from here we get; ${{W}_{net}}={{\left( \sum{Q} \right)}_{cycle}}=10+15-10=15J$
Thus, $\Delta {{Q}_{S}}=10+15-10=15J$
Therefore, $\eta =\dfrac{15}{20}\times 100=60$
Therefore, the correct answer is option C.

Note:
Remember that the thermodynamics cyclic process takes place when a system in each initial state goes in different changes of state and finally returns to its initial state. Some variables in a thermodynamic system are path functions, like work and heat which depend on the path taken.