Question
Question: What will be the contact forces at A and B if the 50kg homogeneous smooth sphere rests on the inclin...
What will be the contact forces at A and B if the 50kg homogeneous smooth sphere rests on the incline A and bears the smooth vertical wall B?
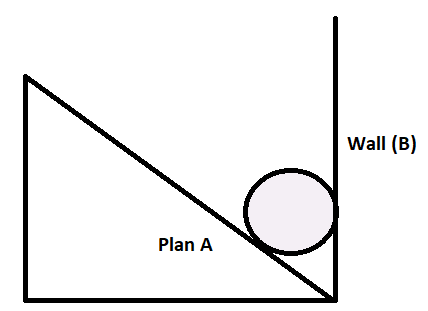
Solution
This problem can be solved by using Lami's theorem. This theorem relates the magnitudes of the coplanar, concurrent and non – collinear forces that maintain an object in static equilibrium. This theorem can be used to analyze mechanical and structural systems.
Complete Step by Step Solution
The statement of Lami’s theorem is –
“When 3 forces performing at a point are in equilibrium, then every force is proportional to the sin of the angle between the opposite 2 forces”.
Lami’s theorem relates the magnitudes of coplanar, synchronal associated non-collinear forces that maintain an object in static equilibrium. The theory is incredibly helpful in analysing most of the mechanical moreover as structural systems.
In mathematics, this theorem can be represented as –
sinαA=sinβB=sinγC
We have to use Lami's theorem in order to solve the question.
According to the question, it is given that, 50 kg homogeneous smooth sphere rests on the incline A and bears the smooth vertical wall B.
Therefore, by using the Lami’s theorem, we get –
⇒sin120∘mg=sin(90∘+60∘)R1=sin90∘R2
Putting the value m=50kg and g=10 in the above equation, we get –
⇒sin(90∘+30∘)50×10=cos60∘R1=1∘R2
From above equation, we can write it as –
⇒sin(90∘+30∘)500=R2 ⇒R2=sin(120∘)500 ⇒R2=31000N
Using the value of R2 for finding the value of R1 , we get –
⇒R1=3500N
Hence, we got the contact forces at A and B as 3500N and 31000N .
Note:
Students often make mistakes while taking angle between components of force. It must be remembered that normal always acts as perpendicular to the surface and point of contact. Therefore, in the case of a sphere, it always passes from the center.
