Question

What will be net resistance between $A$ and $B$?

(A) $\dfrac{3}{2}\left( {\sqrt 5 - 1} \right)\,\Omega$
(B) $\dfrac{3}{2}\left( {\sqrt 5 + 1} \right)\,\Omega$
(C) $\dfrac{{3\sqrt 3 }}{2}$
(D) $3\,\Omega$

Answer 1

Hint By using the resistor in series and resistor in parallel formula, the solution can be determined. Before that one assumption must be made. This circuit goes to an infinity, so that we consider the one loop for our calculation. In the end the result is in equation form, then by using the quadratic equation formula, the solution can be determined.

Useful formula
The resistor in series formula is given by,
$R = {R_1} + {R_2} + ...........$
Where, $R$ is the total resistance of the resistor in series and ${R_1}$, ${R_2}$ are the resistance of the individual resistor.
The resistor in parallel formula is given by,
$\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ...........$
Where, $\dfrac{1}{R}$ is the total resistance of the resistor in parallel and ${R_1}$, ${R_2}$ are the resistance of the individual resistor.

Complete step by step solution
The above given diagram is having same loop but it goes infinitely, so we take only the first loop, so that the first loop contains four resistors.

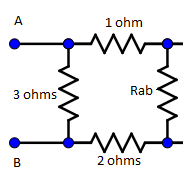
From the above diagram the three resistors are in series, $1\,\Omega$, $2\,\Omega$ and ${R_{AB}}$ are in series, then by using the resistor in series formula, then
$R = 1 + 2 + {R_{AB}}$
By adding the terms in the above equation, then
$R = 3 + {R_{AB}}$
Now, the circuit will be come two resistors and these two resistors are in parallel,

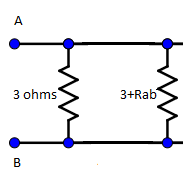
From the above diagram the two resistors are in parallel, so by using the resistors in parallel formula, then
$\dfrac{1}{{{R_{AB}}}} = \dfrac{1}{3} + \dfrac{1}{{\left( {3 + {R_{AB}}} \right)}}$
By cross multiplying the terms in the above equation, then
$\dfrac{1}{{{R_{AB}}}} = \dfrac{{3 + {R_{AB}} + 3}}{{3\left( {3 + {R_{AB}}} \right)}}$
On further simplification in the above equation, then
$\dfrac{1}{{{R_{AB}}}} = \dfrac{{{R_{AB}} + 6}}{{9 + 3{R_{AB}}}}$
By cross multiplying the terms in the above equation, then
$9 + 3{R_{AB}} = {R_{AB}}\left( {{R_{AB}} + 6} \right)$
On multiplying the terms in the above equation, then
$9 + 3{R_{AB}} = {R_{AB}}^2 + 6{R_{AB}}$
By rearranging the terms in the above equation, then
${R_{AB}}^2 + 3{R_{AB}} - 9 = 0$
This equation is in the form of a quadratic equation.
From the above equation, the values of $a = 1$, $b = 3$ and $c = - 9$, these values are the coefficient of equations.
The formula to solve the quadratic equation is, ${R_{AB}} = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$
Now substituting the values of $a$, $b$ and $c$ in the above equation, then
${R_{AB}} = \dfrac{{ - 3 \pm \sqrt {{3^2} - \left( {4 \times 1 \times - 9} \right)} }}{{2 \times 1}}$
On multiplying the terms in the above equation, then
${R_{AB}} = \dfrac{{ - 3 \pm \sqrt {9 + 36} }}{{2 \times 1}}$
On adding the terms in the above equation, then
${R_{AB}} = \dfrac{{ - 3 \pm \sqrt {45} }}{{2 \times 1}}$
The above equation is also written as,
${R_{AB}} = \dfrac{{ - 3 \pm \sqrt {9 \times 5} }}{{2 \times 1}}$
By taking the square root in the above equation, then
${R_{AB}} = \dfrac{{ - 3 \pm 3\sqrt 5 }}{2}$
By taking the common terms in the above equation, then
${R_{AB}} = \dfrac{3}{2}\left( { - 1 \pm \sqrt 5 } \right)$
Then the above equation is written as,
${R_{AB}} = \dfrac{3}{2}\left( {\sqrt 5 - 1} \right)\,\Omega$

Hence, the option (A) is the correct answer.

Note The circuits given in the question are infinite loop so that we take one loop in the given circuit and the calculations are made. By using the resistor in series and resistors in parallel formula, just check the registers that are in series are parallel thoroughly.