Question
Question: What should be the value of \(M\) so that the block does not slide over the triangular wedge? All su...
What should be the value of M so that the block does not slide over the triangular wedge? All surfaces are smooth.
A. 54(3−1)m
B. 4(3+1)m
C. 25(3+1)m
D. 5(3−1)m
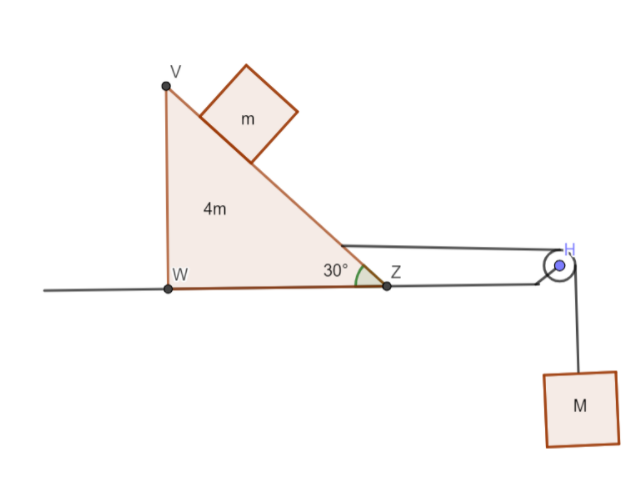
Solution
Pseudo force is used whenever there is a relative motion with different accelerations. Tension acting along a string does not change till the time the string encounters a new acceleration or has some object. However, the acceleration in the string remains unchanged.
The acceleration with which the whole wedge mass system moves is given by a=gtanθ where a is the acceleration and θ is the angle between the wedge sides. This angle is also the angle of inclination for the mass m kept on the wedge.
Under the equilibrium condition, the body experiences balanced force in all directions and does not undergo motion. When all surfaces are smooth, it means that the frictional force is absent and its effect should be neglected.
Complete step by step solution:
We will first visualize the forces using a free body diagram of the mass m given in the question.
The free body diagram is given below
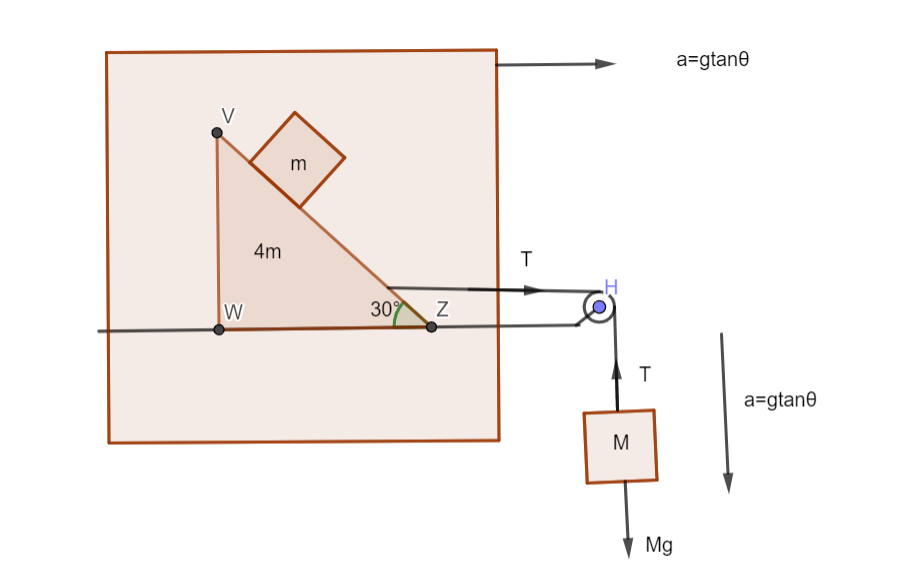
Here θ=300 as per the given question.
For the vertical equilibrium,
Mg−T=Ma,
Substituting a=gtanθ we get,
Mg−T=Mgtanθ .
This becomes our force equation.
For the horizontal equilibrium,
T=(4m+m)a
Again substituting a=gtanθ we get,
T=5mgtanθ
Substituting this in the force equation we get,
Mg−5mgtanθ=Mgtanθ
Cancelling out the common terms and substituting θ=300 ,
M−5mtan300=Mtan300
⇒M−5m31=M31
Rearranging the terms we get,
M(1−31)=5m×31
Further solving the equation, we get,
M=3−15m .
Rationalizing this,
M=3−15m×3+13+1
⇒M=25(3+1)m
Hence, C is the correct option.
Note:
Here we have used the term acceleration while calculating the forces. But this term in effect means the effective acceleration experienced by the whole system under consideration. And thus, it was the same for the string as well as for the wedge mass system. We must balance the forces in both x and y directions to get every equation we would need to solve. Else we might not get sufficient information from the free body diagram to solve the question.
