Question

What should be the minimum value of the refractive index of a prism, refracting angle $A$, so that there is no emergent ray irrespective of the angle of incidence?

Answer 1

Let us first get some idea about prism. An optical prism is a light-refracting transparent optical device having flat, polished surfaces. Prisms must have at least one angled surface; objects with two parallel surfaces are not prisms. The typical geometrical shape of an optical prism is a triangular prism with a triangular base and rectangular sides, and "prism" is commonly used to refer to this sort of prism.

Complete step by step answer:
The refractive index of a substance (also known as refraction index or index of refraction) is a dimensionless quantity that specifies how fast light passes through it in optics. When light enters a material, the refractive index influences how much the path of light is bent, or refracted.

The angle of incidence and refraction of a ray crossing the interface between two media with refractive indices of ${n_1}$ and ${n_2}$ are described by Snell's law of refraction, ${n_1}sin{\theta _1}{\text{ }} = {\text{ }}{n_2}sin{\theta _2}$
where ${\theta _1}$ and ${\theta _2}$ are the angles of incidence and refraction, respectively, of a ray crossing the interface between two media with refractive indices of ${n_1}$ and ${n_2}$.

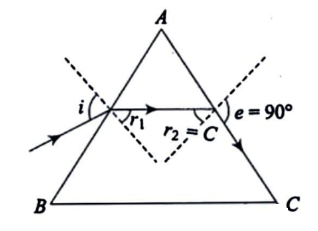
Now let’s solve the problem: the ray emerges from $AC$ face.
As given in the figure:
$e = {90^ \circ },{r_2} = C$
And we can say from the diagram:
$A = {r_1} + {r_2} = {r_1} + C$
As we discussed above about the Snell’s law so if we apply this on the face $AB$ we will get:
$\sin \,i = n\sin {r_1}$ ....$eq(1)$

According to $eq(1)$, n is the smallest when ${r_1}$is the greatest, i.e. ${r_2} = C.{\text{ }}i = {90^ \circ }$in this case.
$A = {r_1} + {r_2} = {r_1} + C$
$\Rightarrow A = 2C\,\,\,or\,\,C = \dfrac{A}{2}$
$\Rightarrow \sin \,i = n\sin {r_1}$
$\Rightarrow 1 = n\sin C$
$\Rightarrow n = \dfrac{1}{{\sin \dfrac{A}{2}}}$
$\therefore n = \cos ec\dfrac{A}{2}$

Note: Let us know some more points regarding refractive index. The refractive indices also govern how much light is reflected at the interface, as well as the critical angle for total internal reflection, intensity (Fresnel's equations), and Brewster's angle.