Question

What should be the closest approximate radius of a celestial body twice as massive as the Sun so that escape speed from the celestial body is equal to the speed of the Sun? (The mass of Sun is $2 \times {10^8}{\text{ }}kg$, speed of light is $3 \times {10^8}{\text{ }}\dfrac{m}{s}$, and Universal Gravitational Constant $G$ $= 7 \times {10^{ - 11}}{\text{ }}\dfrac{{N.{m^2}}}{{k{g^2}}}$)
A. $300{\text{ }}km$
B. ${\text{1 }}km$
C. $90{\text{ }}km$
D. ${\text{6 }}km$

Answer 1

Escape speed or velocity refers to that velocity with which a body escapes to infinity. We have to derive the formula by which we can find the escape velocity. This can be found with the help of total energy of the system which remains constant. The total initial kinetic and potential will be equal to the total final kinetic and potential energy.

Complete step by step answer:

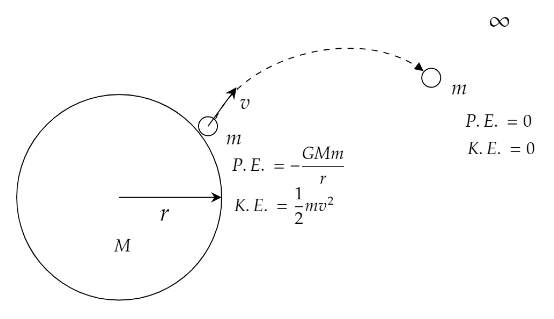
By the conservation of energy we get,
Initial Kinetic Energy$+$Initial potential energy$=$ Final Kinetic energy$+$ Final potential energy.
The initial potential energy of the celestial body is given as $- \dfrac{{GMm}}{r}$.The variables are declared as, $G =$ Universal Gravitational Constant, $M =$ Mass of the celestial body, $m =$ mass of the body that needs to escape from the celestial body and $r =$ radius of the celestial body.

The initial kinetic energy is given as $\dfrac{1}{2}m{v^2}$.The variables are declared as,
$m =$ mass of the body that needs to escape from the celestial body and $v =$ the escape velocity.
The final potential energy is $0$ as the distance between the body and the celestial body is infinity.When the object is at infinity, its final velocity is $0$.Substituting the values in energy conservation we get,
$- \dfrac{{GMm}}{r} + \dfrac{1}{2}m{v^2} = 0 + 0$
Simplifying the given equation we get,
$v = \sqrt {\dfrac{{2GM}}{r}} - - - - \left( 1 \right)$
This is the escape velocity.

Given in the question,
$M =$ mass of celestial object$= 2 \times$ Mass of the Sun$= 4 \times {10^{30}}{\text{ }}kg$
$G =$ Universal Gravitational Constant$= 7 \times {10^{ - 11}}{\text{ }}\dfrac{{N.{m^2}}}{{k{g^2}}}$
$v =$ velocity of light$= 3 \times {10^8}{\text{ }}\dfrac{m}{s}$
Substituting all the values in equation $\left( 1 \right)$ we will find the radius $r$ ,
$3 \times {10^8} = \sqrt {\dfrac{{2 \times 7 \times {{10}^{ - 11}} \times {\text{4}} \times {\text{1}}{{\text{0}}^{30}}{\text{ }}}}{r}}$
Squaring both sides we get,
$9 \times {10^{16}} = \dfrac{{56 \times {{10}^{19}}}}{r}$
By cross-multiplication we get,
$r = \dfrac{{56 \times {{10}^{19}}}}{{9 \times {{10}^{16}}}} \\\ \therefore r= 6.22 \times {10^3}$
Thus, the radius of the celestial body is $6.22{\text{ }}km$.

Hence, the correct answer is option D.

Note: It must be noted that the value of Universal Gravitational Constant is always the same for any place in the space. If the escape velocity of any body is the same as the velocity it is assumed that it will be caught up in the singularity of time. The escape velocity of black hole is greater than the speed of light. It also does not allow light to escape from its gravity.