Question

What should be the angle of banking of a circular track of radius 600m which is designed for cars at an average speed of 180 km/h ?

Answer 1

In force / acceleration problems we try to generate the equation by balancing the forces like if the body moving of the ground there will be no vertical acceleration, if the body is in on the inclined plane and body don’t slips then the weight gets normalized with the component of Normal reaction of the inclined plane. By solving those equations we get the value of the angle of inclination is $\theta$.

Step by step solution :- An image is drawn to depict the situation here the angle of inclination is $\theta$.

 ![](https://www.vedantu.com/question-sets/f06b81e5-3d2f-4fbf-8083-dfdffce90c8a6043658874962200948.png)  

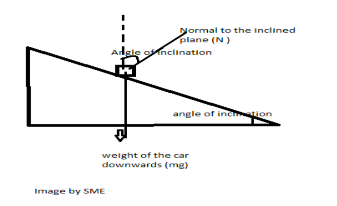
The forces acting on the car are
Weight of the car (mg) , which is acting downwards and
The normal force (N)
For vertical direction the acceleration is zero.
So, the balancing equation becomes
$\Rightarrow N\cos \theta = Mg$……………. Eq.(1)
For horizontal direction, the acceleration is $\dfrac{{{v^2}}}{r}$, and it is acting towards the centre because when a body moves in a circle there is an acceleration (a=$\dfrac{{{v^2}}}{r}$) acting on the body towards the centre.
So , the balancing equation becomes
$\Rightarrow N\sin \theta = \dfrac{{M{v^2}}}{r}$……………… Eq.(2)
By performing the operation Eq.(2) / Eq.(1) , we get
$\Rightarrow \dfrac{{N\sin \theta }}{{N\cos \theta }} = \dfrac{{M{v^2}}}{{r.Mg}}$
Simplifying the relation , we get
$\Rightarrow \tan \theta = \dfrac{{{v^2}}}{{rg}}$ ………………Eq.(3) ; here we have to put the value of velocity in m/s .
$\Rightarrow v = 180\dfrac{{km}}{{hr}}$; converting it to m/s , we get
$\Rightarrow v = 180\dfrac{{km}}{{hr}} = 180 \times \dfrac{{1000m}}{{3600\sec }}$
Further simplifying the equation we get with
$\Rightarrow 180\dfrac{{km}}{{hr}} = 50dfrac{m}{{\sec }}$
$\Rightarrow v = 50\dfrac{m}{{\sec }}$ ; $\ r = 600m \\\ g = 9.8m/{s^2} \\\ \$ ……… putting all the values in Eq.(3) we get
$\Rightarrow \tan \theta = \dfrac{{{{(50)}^2}}}{{600(9.8)}}$
Further simplifying the equation we get with
$\Rightarrow \tan \theta = 0.4251$
Further simplifying the equation we get with
$\Rightarrow \theta = {\tan ^{ - 1}}(0.4251) = 23.03^\circ$
$\Rightarrow \theta = 23.03^\circ$
Hence, the angle of banking of a circular track of radius 600m which is designed for cars at an average speed of 180 km/h should be $\theta = 23.03^\circ$.

Note:- Many racing tracks are banked turns that means they are sloped to keep the race cars tilted inwards. These banks are both safer and faster than flat roads . The race cars which can reach faster velocity than 200 mph can be off the track if banking is not provided.