Question

What line is perpendicular to $y = - 3$ and passes through point $\left( {4, - 6} \right)$?

Answer 1

We are supposed to find the equation of line that is perpendicular to$y = - 3$. Here, $y = - 3$ is a horizontal line. So the line perpendicular to this equation must be a vertical line. Also it must be passing through point $\left( {4, - 6} \right)$. So, let us look at the graphs below and find out the equation.

Complete step by step solution:
In this question, we are given an equation of line $y = - 3$ and we are supposed to find another equation of line that is perpendicular to this line and also passes through the point $\left( {4, - 6} \right)$.
Now, first of all let us draw the graph for $y = - 3$.

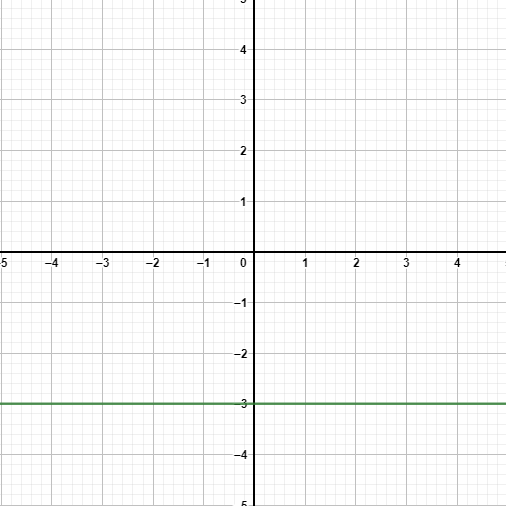
Here, we can see that the equation $y = - 3$ is of a straight horizontal line. So, the line that will be perpendicular to this equation must be a vertical line.
And also, it is given that the vertical line should be passing through point $\left( {4, - 6} \right)$.
So therefore, $x = 4$ will be perpendicular to the given line $y = - 3$ and will be passing through the point $\left( {4, - 6} \right)$.
Let us draw the graph for $x = 4$ and see whether our answer is correct or not.

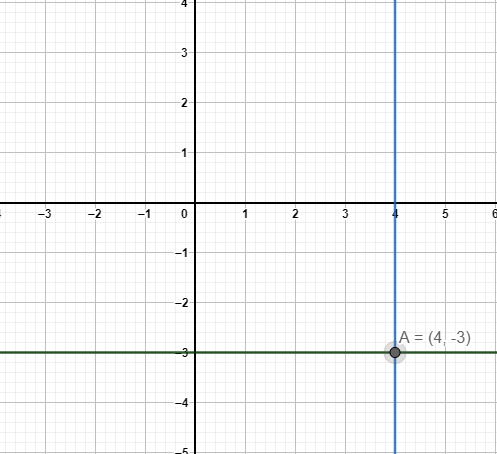
Here, in this graph we can see that the line $x = 4$ is perpendicular to the line $y = - 3$ and it is passing through the x coordinate 4.
Hence, our answer is correct.

Note:

Note that if you are asked to find a line parallel to the given line that line must be a horizontal line and if the given line is also horizontal line, then it must not intersect the given line.
Also, remember that the product of slopes of two perpendicular lines is always equal to $- 1$.