Question

What is Unit Vector ?

Answer 1

In order to understand the answer of this problem let us first get some knowledge about vectors. A quantity that has both a direction which is a magnitude, and is used to determine the relative location of two points in space is called a vector.

Complete step by step answer:
A vector is a quantity that has both a magnitude and a direction associated with it. A unit vector is a vector with a magnitude of one. It's often referred to as a Direction Vector. By dividing any vector by the magnitude of the given vector, it can be converted to a unit vector.

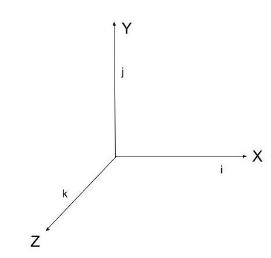
Unit vector is represented by the symbol which is called a cap or hat. It is given by
$\hat u = \dfrac{u}{{|u|}}$
Here, $\hat u =$normalized vector, $u =$Non-zero vector and $|u| =$Norm (or length) of $u$.

At a given point, the normal vector is a vector that is perpendicular to the earth. It's also known as "normal," and it's a vector that extends to a surface. We know that usually,$xyz$coordinates are used to write any vector.
$\vec a = x\hat i + y\hat j + z\hat k$
Formula for magnitude of a vector is:
$|\vec a| = \sqrt {{x^2} + {y^2} + {z^2}}$
$\text{Unit Vector} =\dfrac{\text{vector}}{\text{vector’s magnitude}}$

Note: These unit vectors are widely used to indicate direction, with the magnitude provided by a scalar coefficient. The sum of unit vectors and scalar coefficients can then be written as a vector decomposition.