Question

What is the y-coordinate of a vertex of a parabola with the following equation $y = {x^2} - 8x + 18$ ?

Answer 1

Hint : To simplify this question , we need to solve it step by step . In order to solve and write the find the vertex of a quadratic equation . We will use the vertex formula and determine the y- coordinate of the vertex of a parabola in simplest form by using the formula $\left( { - \dfrac{b}{{2a}},f(x)} \right)$ . We will first determine the x-coordinate and then we fill substitute the found x-coordinate in the quadratic equation to determine y-coordinate of the vertex of a parabola with the following equation $y = {x^2} - 8x + 18$
We can also use the quadratic in vertex form method to get our required result.

Complete step-by-step answer :
A quadratic equation is written as $a{x^2} + bx + c$ in its standard form . As we know that in the quadratic equation , a is the coefficient of the first term in the quadratic, b is the coefficient of the second term and c is the coefficient of the third term in the quadratic.
Now we are Assessing the coefficients of our quadratic equation given $y = {x^2} - 8x + 18$
The values of a, b and c are as follows =.
$a = 1 \\\ b = - 8 \\\ c = 18 \;$
And the vertex can be found by using the formula $\left( { - \dfrac{b}{{2a}}} \right)$
Vertex = $\left( { - \dfrac{b}{{2a}},f(x)} \right)$
Now , we will substitute the values in this formula we get
$\left( { - \dfrac{b}{{2a}}} \right) \\\ \Rightarrow - \dfrac{{( - 8)}}{{2 \times 1}} \\\ \Rightarrow \dfrac{8}{2} \\\ \Rightarrow 4 \;$
This 4 is the required x-coordinate of the vertex of parabola .
Now , looking at the formula of Vertex $\left( { - \dfrac{b}{{2a}},f(x)} \right)$ , we got x- coordinate . We will be substituting the x-coordinate into the given quadratic equation $y = {x^2} - 8x + 18$ to get the required y-coordinate of the vertex of the parabola

By Substituting , we get-
Vertex = $\left( { - \dfrac{b}{{2a}},f(x)} \right)$
This formula becomes and when simplifying further , we will get vertex .

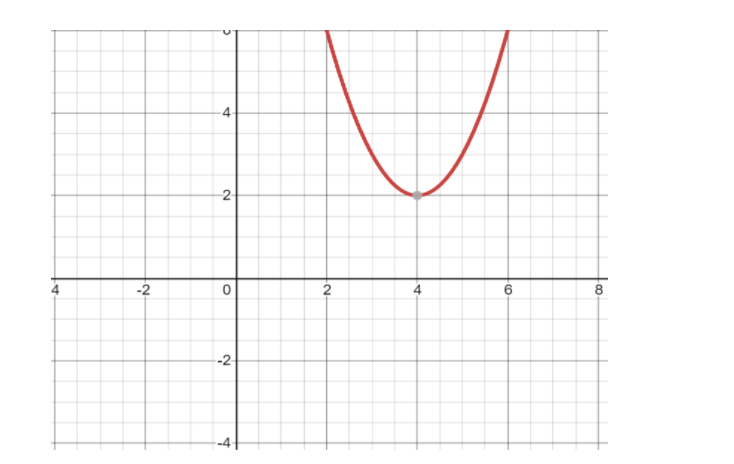
Vertex = $(4,2)$
Therefore , $(4,2)$ is the required vertex and 2 is the required y-coordinate of the vertex of the parabola with the quadratic equation $y = {x^2} - 8x + 18$ .

Note : If $a > 0$, the parabola opens upward. If $a < 0$ , the parabola opens downward.
The general form of a parabola to find the equation for the axis of symmetry.
The axis of symmetry is defined by $x = \left( { - \dfrac{b}{{2a}}} \right)$ .
The vertex of a parabola will be either a maximum or a minimum, the range will consist of all y-values greater than or equal to the y-coordinate of the vertex or less than or equal to the y-coordinate at the turning point, depending on whether the parabola opens up or down.
Always try to understand the mathematical statement carefully and keep things distinct .