Question

What is the vertex of the parabola $y = 4x - {x^2}$?

Answer 1

In this question, we have to find the vertex for the given parabola.
For doing that first we have to differentiate the given equation of the parabola with respect to x. Then making that first derivative equals to zero we will get the x coordinate of the vertex. Putting that in the equation of the parabola we will get the value of y and hence the vertex.
Formula:
Differentiation formula:
$\dfrac{{d{x^n}}}{{dx}} = n{x^{n - 1}}$

Complete step-by-step solution:
In this question we have to find out the vertex of the parabola $y = 4x - {x^2}$.
A parabola only has one vertex, which may be a maximum or a minimum. To find it, we must derive it and equal it to zero.

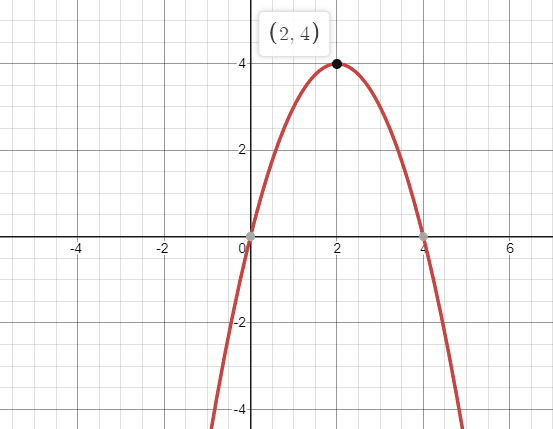
We need to find out the derivative of $y = 4x - {x^2}$ with respect to x,
Differentiating we get, $\dfrac{{dy}}{{dx}} = 4 - 2x$.
[using the formula, $\dfrac{{d{x^n}}}{{dx}} = n{x^{n - 1}}$]
Now we need to equate the first derivative equals to zero to find the x coordinate of the vertex
We get, $4 - 2x = 0$
Or, $2x = 4$
Or, $x = \dfrac{4}{2} = 2$
Now we get the x coordinate of the vertex is $2$.
To find the y coordinate of the vertex we need to put $x = 2$ in the equation of the parabola $y = 4x - {x^2}$.
We get,

&y; = 4 \times 2 - {2^2} \\\ & = 8 - 4 \\\ & = 4 \\\ \end{aligned} $$. **Hence the vertex of the parabola $$y = 4x - {x^2}$$ is $$(2,4)$$.** **Note:** The derivative of a function of a real variable measures the sensitivity to change of the function value with respect to a change in its argument. Derivatives are a fundamental tool of calculus. Derivative of a function $$y = f\left( x \right)$$can be written as $$\dfrac{{dy}}{{dx}}$$ or $$f'\left( x \right)$$. Here by the graph of parabola we can see that at the vertex we get the maximum value. We could also find out the nature by the second derivative. Parabola: A parabola is a U-shaped plane curve where any point is at an equal distance from a fixed point (known as the focus) and from a fixed straight line which is known as the directrix.