Question

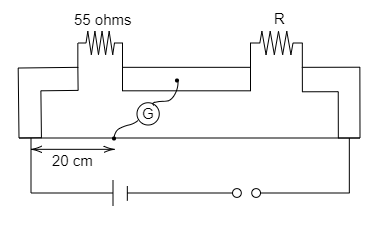
What is the value of unknown resistance $R$, if the galvanometer shows null deflection in the given meter bridge set up shown in the fig?

(A) $97.50\,\Omega$
(B) $105\,\Omega$
(C) $220\,\Omega$
(D) $110\,\Omega$

Answer 1

The value of the unknown resistance can be determined by using the wheatstone bridge principle. The wheatstone bridge principle shows the relation between the resistance which are connected in the circuit. By using the wheatstone bridge principle, the unknown resistance is determined.
Useful formula:
The wheatstone bridge principle is given by,
$\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{R_3}}}{{{R_4}}}$
Where ${R_1}$, ${R_2}$, ${R_3}$ and ${R_4}$ are the resistance which are connected in the same circuit.

Complete answer:
Given that,
The resistance of the first resistor is, ${R_1} = 20k\,\Omega$,
Where, $k$ is the resistance per unit length. The one end of the galvanometer is connected in $20\,cm$ length. And assume the total length is $100\,cm$.
The resistance of the second resistor is, ${R_2} = 55\,\Omega$,
The resistance of the third resistor is, ${R_3} = 80k\,\Omega$,
The resistance of the fourth resistor is, ${R_4} = R\,\Omega$.
Now,
The wheatstone bridge principle is given by,
$\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{R_3}}}{{{R_4}}}\,.....................\left( 1 \right)$
By substituting the four resistance values in the above equation, then the above equation is written as,
$\dfrac{{20k}}{{55}} = \dfrac{{80k}}{R}$
By cancelling the same terms in the above equation, then the above equation is written as,
$\dfrac{{20}}{{55}} = \dfrac{{80}}{R}$
By rearranging the terms in the above equation, then the above equation is written as,
$R = \dfrac{{80 \times 55}}{{20}}$
By multiplying the terms in the above equation, then the above equation is written as,
$R = \dfrac{{4400}}{{20}}$
By dividing the terms in the above equation, then the above equation is written as,
$R = 220\,\Omega$

Hence, the option (C) is the correct answer.

Note:
If the galvanometer shows the null deflection, then the given circuit is considered as the wheat stone bridge because in the wheatstone bridge, there are four resistors connected and it will be balanced on both sides. The same logic is used here.