Question

What is the value of the shunt resistance if $10\%$ of the main current passing through the galvanometer of resistance $99\Omega$?

& A.11\Omega \\\ & B.0.11\Omega \\\ & C.1.1\Omega \\\ & D.110\Omega \\\ \end{aligned}$$

Answer 1

We know that a galvanometer is an instrument which can detect the electric current in a circuit. We can convert a moving coil galvanometer into a voltmeter or an ammeter by adding a resistance to the circuit. If follows the principle, that when a current carrying coil is kept in the proximity of a magnetic field it experiences a torque.

Formula used:
$\dfrac{S}{G}=\dfrac{i_{g}}{i-i_{g}}$

Complete step-by-step answer:
A galvanometer works on the principle of electromagnetic induction, which is when a current carrying conductor is placed in a magnetic field, it experiences a torque. A galvanometer when connected in parallel to a circuit with low resistance, it can act as an ammeter and measure the current in that circuit. This low resistance is also called the shunt resistance.
Let us assume that a shunt $S$ is connected in parallel with a galvanometer with resistance $G$, then we know that the current in the circuit gets divided. If $i$ is the total current in the circuit and $i_{g}$ is the current in the galvanometer, then the current flowing through the shunt resistance is given as $i_{s}=i-i_{g}$.
Given that, $i_{g}=0.1i$ and $G=99\Omega$ .

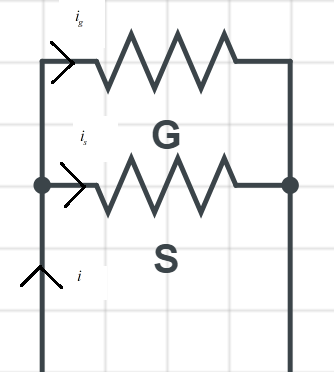
Since the voltage in both the circuit are equal, we also know from ohms law that $V=IR$.Applying the same, we $\dfrac{S}{G}=\dfrac{i_{g}}{i-i_{g}}$.
Substituting the values, we get, $S=\dfrac{0.1i}{i-0.1i}\times 99$
$\implies S=\dfrac{0.1}{0.99}\times 99= 1.1\Omega$
Hence the answer is option $C.1.1\Omega$

So, the correct answer is “Option C”.

Note: We know that the sensitivity of a galvanometer is its ability to give large deflections even for a small value of the current. And it is given as the ratio between the change deflections in the galvanometer to the change in current in the coil galvanometer. The torque experienced by the current conductor in the magnetic field causes the pointer in the galvanometer to show deflection in the reading of the galvanometer.