Question

What is the value of the resistance R needed to make ${{V}_{0}}=4V$?

Answer 1

When we analyze a combination of the resistor in a circuit, the voltage drop across the resistors connected parallel to each other is always the same. Whereas the current among the series-connected resistors is always the same. This circuit analysis is very important in solving complex circuits and analyzing their characters.
Formula used:
$V={{V}_{1}}+{{V}_{2}}$
${{V}_{1}}={{V}_{in}}\left( \dfrac{{{R}_{1}}}{{{R}_{1}}+{{R}_{2}}} \right)$

Complete step by step solution:
When the resistors are connected in series the total voltage drop across the circuit is given as,
$V={{V}_{1}}+{{V}_{2}}+...$
And the value of current along all the resistors connected in series is always constant.
On the other hand, if we see the parallel-connected resistors, the voltage drop across each resistor is the same but there is a change in the current in each resistor.
To the total value of current going into resistors which are connected parallel to each other is given as,
$I={{I}_{1}}+{{I}_{2}}+{{I}_{3}}+...$
The combination of resistors in the circuit mentioned in the question can be reconstructed as the diagram shown here,

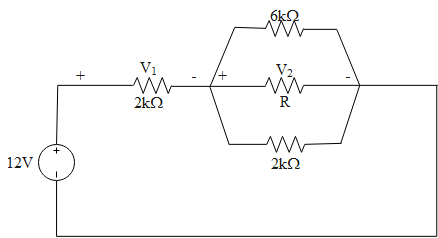
The value of voltage across the resistors connected parallel always remains the same. So if we have to achieve a voltage drop $4V$ along with the $6k\Omega$ resistor. Then the voltage across the resistor $R$ must be $4V$.
In this case, the voltage across the resistor $2\Omega$ will be,
$\begin{aligned} & {{V}_{in}}={{V}_{1}}+{{V}_{2}} \\\ & \Rightarrow 12={{V}_{1}}-4 \\\ & \Rightarrow {{V}_{1}}=8V\quad .....(1) \\\ \end{aligned}$
By the voltage divider theorem, the voltage across $2k\Omega$ is given as,
${{V}_{1}}={{V}_{in}}\left( \dfrac{{{R}_{1}}}{{{R}_{1}}+{{R}_{2}}} \right)\quad ......(2)$
From equation (1) and (2),

& 8=12\left( \dfrac{2\times {{10}^{3}}}{2\times {{10}^{3}}+{{R}_{eq}}} \right) \\\ & \Rightarrow 16\times {{10}^{3}}+8{{R}_{eq}}=24\times {{10}^{3}} \\\ & \Rightarrow 8{{R}_{eq}}=8\times {{10}^{3}} \\\ & \therefore {{R}_{eq}}=1000\Omega =1k\Omega \\\ \end{aligned}$$ So the equivalent resistance of the three resistors $\left( R,6k\Omega ,2k\Omega \right)$ which are in parallel to each other So from this, we can say that, $\begin{aligned} & \dfrac{1}{1k}=\dfrac{1}{R}+\dfrac{1}{6k}+\dfrac{1}{2k} \\\ & \Rightarrow \dfrac{12+8R}{12R}=1 \\\ & \Rightarrow 4R=12k \\\ & \therefore R=3k\Omega \\\ \end{aligned}$ **Thus the required value of the resistor is $3k\Omega$** **Note:** Resistor is considered to be a linear passive component. It is the only passive component which obeys ohm’s law. According to this law, the voltage drop across a resistor is directly proportional to the current flowing through the resistor.