Question

What is the value of the force F to be applied horizontally on a block of mass$5$ kg which is in contact with a wall, as shown in the figure. (Take g= $10m{s^{ - 2}}$ ) such that it does not fall down. The coefficient of friction between the block and the wall is $0.4$ .

Answer 1

To solve questions related to friction and gravity, we need to understand the concept of direction of frictional force. Also, we need to understand how the pair of action reactions works and draw Free body diagrams to represent the body and the different forces acting on it.

Complete step by step solution:
First, draw the free body diagram of the situation.

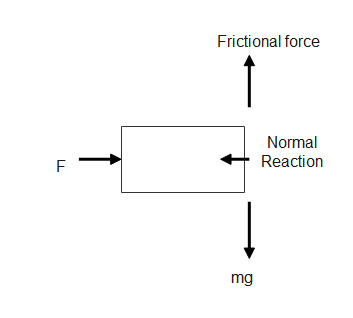
Drawing the free body diagram, we see that if we want the body to remain in equilibrium, the frictional force between the wall and the body has to be greater enough to balance the body’s weight which is acting downwards. Now we also know that the value of frictional force is dependent on Normal reaction. Thus, we have to find the value of a normal reaction at first.
From the Free body diagram, we see that there is no horizontal net force, as the body is pressed against the wall, thus net horizontal force is zero.
Thus, $F = {\text{ N}}$
We know frictional force F is equal to $\mu N$ , where $\mu$ is the coefficient of friction and $N$ is the normal reaction.
Now according to observation, frictional force equals the weight of the body, thus:
$f = mg$ and $f =$ $\mu N$
Thus, $\mu N = mg$ .
We are given the values of mass of the body ($5$ kg) and the value of acceleration due to gravity ( $10m{s^{ - 2}}$ ) and coefficient of friction( $0.4$ ).
Thus $N = \dfrac{{mg}}{\mu }$
= $125$ N. As $F = {\text{ N}}$ thus Force equals $125$ N.

Hence the correct option is option D.

Note: Please ensure that before starting to workout this problem you draw the Free body diagram of the body as it will give us a clear idea of all the forces. We often make mistakes in considering the normal reaction, so see all the forces carefully and then consider it. All the listed formulas are to be remembered.