Question

What is the value of the expression $\dfrac{\tan x}{x}$ at x = 0.
(a) $\dfrac{0}{0}$
(b) $\dfrac{\infty }{\infty }$
(c) $\infty \times \infty$
(d) None of the above

Answer 1

Hint : To solve this question, we will first find the value of tanx at various values x. We shall be dealing the values of x in radiance and not in degrees. Then we will divide the value of tanx with x at x = 0 and find which of the given options matches our answer. To understand the answer much better, we also draw the graph of $\dfrac{\tan x}{x}$.

Complete step-by-step answer :
To begin with, we will define the value of tanx at 0, $\dfrac{\pi }{6}$, $\dfrac{\pi }{4}$, $\dfrac{\pi }{3}$ and $\dfrac{\pi }{2}$.
At x = 0, tanx = 0
At x = $\dfrac{\pi }{6}$, tanx = $\dfrac{1}{\sqrt{3}}$
At x = $\dfrac{\pi }{4}$, tanx = 1
At x = $\dfrac{\pi }{3}$, tanx = $\sqrt{3}$
At x = $\dfrac{\pi }{2}$, tanx = not defined
Now, we will substitute x = 0 in the expression $\dfrac{\tan x}{x}$.
$\Rightarrow \dfrac{\tan 0}{0}$
But we know that x = 0, tanx = 0
So, $\dfrac{\tan 0}{0}=\dfrac{0}{0}$
But this is an indeterminate form and cannot be treated as a solution.
Therefore, we apply limits x tends to 0 on $\dfrac{\tan x}{x}$
$\begin{aligned} & \Rightarrow \underset{x\to 0}{\mathop{\lim }}\,\dfrac{\tan x}{x} \\\ & \Rightarrow \underset{x\to 0}{\mathop{\lim }}\,\dfrac{\sin x}{x}\times \dfrac{1}{\cos x} \\\ \end{aligned}$
At x = 0, cosx = 1
We apply L’hospital’s rule on $\underset{x\to 0}{\mathop{\lim }}\,\dfrac{\sin x}{x}$ . According to L’hospital’s rule, we will derivate the numerator and denominator wrt x.
$\begin{aligned} & \Rightarrow \underset{x\to 0}{\mathop{\lim }}\,\dfrac{\cos x}{1} \\\ & \Rightarrow 1 \\\ \end{aligned}$
Hence, as x tends to 0, $\dfrac{\tan x}{x}$ = 1.
We will also see the graph of $\dfrac{\tan x}{x}$
The graph is as follows:

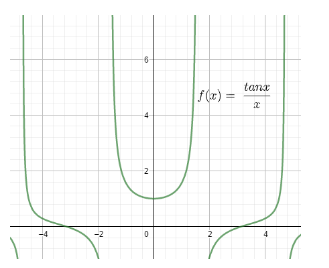
In the graph, as x approaches 0, the value of the function $\dfrac{\tan x}{x}$ approaches 1.
So, the correct answer is “Option A”.

Note : Students are advised to remember the values of trigonometric ratios at general angles. The values like $\infty$, $\dfrac{0}{0}$, $\dfrac{\infty }{\infty }$ and $\infty \times \infty$ are undefined values and they do not logically exist in mathematics. So, if an expression is reduced to one of the aforementioned expressions, we make use of limits. If we are defining it as limit x tends to 0, this means that x is very close to 0 but not exactly zero.