Question
Question: What is the value of tangential acceleration in U.C.M?...
What is the value of tangential acceleration in U.C.M?
Solution
Hint: In this question take into consideration of the two acceleration faced by the body undergoing a circular motion, one that is centripetal acceleration which is directed towards the center of the circular motion and other one that is tangential acceleration which acts tangentially at the specific point where the object is present. This will help approaching the problem.
Step By Step Answer:
U.C.M refers to uniform circular motion.
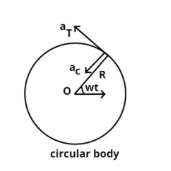
Whenever a body is revolting in a circle as shown in the figure they feel two types of acceleration which is given below:
(i) Centripetal acceleration – Centripetal force is always directed towards the center as shown in the figure this is the minimum required force to hold the body in circular motion.
Due to this force a centripetal acceleration is working towards the center of the circle as shown in the figure denoted by aC.
(ii) Tangential acceleration – Tangential acceleration is always tangent to the body in a circular motion as shown in the figure denoted by aT.
Now there are two types of circular motion which is given below:
(i) Uniform circular motion – In this type of motion the body rotational speed does not changes i.e. direction of the rotation changes at every moment but magnitude remain same in this case the value of tangential acceleration is zero as there is no change in the magnitude of the rotational speed of the body.
(ii) Non-uniform circular motion – In this type of motion the body rotational speed changes i.e. direction of the rotation changes at every moment and the magnitude of the rotational speed also changes, in this case the value of tangential acceleration is non- zero as there is a significant changes in the magnitude of the rotational speed of the body.
Thus the value of tangential acceleration in case of U.C.M is zero.
Note: One can easily be confused stating that the acceleration is simply the rate of change of velocity and since in circular motion the velocity changes at every point of the circular motion so the tangential acceleration can’t be zero. The fact that since the motion we are talking about is uniform circular motion thus although the direction of velocity keeps on changing but the magnitude remains constant throughout and thus if we differentiate this constant with respect to time to obtain acceleration, differentiation of the constant will eventually be zero.
