Solveeit Logo
Login

Question

Question: What is the value of \(\tan {7^ \circ }\tan {23^ \circ }\tan {60^ \circ }\tan {67^ \circ }\tan {83^ ...

What is the value of tan⁡7∘tan⁡23∘tan⁡60∘tan⁡67∘tan⁡83∘\tan {7^ \circ }\tan {23^ \circ }\tan {60^ \circ }\tan {67^ \circ }\tan {83^ \circ }?
a) 13 b) 3 c) 1 d) ∞  a)\,\dfrac{1}{{\sqrt 3 }} \\\ b)\,\sqrt 3 \\\ c)\,1 \\\ d)\,\infty \\\

Explanation

Solution

You should know that tan⁡(90−θ)=cot⁡θ   &  tan⁡θ=1cot⁡θ \tan \left( {90 - \theta } \right) = \cot \theta \,\,\,\& \,\,\tan \theta = \dfrac{1}{{\cot \theta }}\,or tan⁡θ.cot⁡θ=1\tan \theta . \cot \theta = 1 using these formulas you can get the required answer.

Formula used:
Complete step-by-step answer:
According to the question we need to find the value of tan⁡7∘tan⁡23∘tan⁡60∘tan⁡67∘tan⁡83∘\tan {7^ \circ }\tan {23^ \circ }\tan {60^ \circ }\tan {67^ \circ }\tan {83^ \circ }
So as we know that the table that is given below:

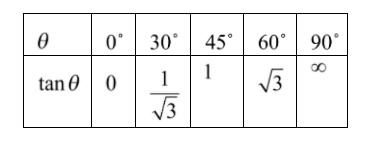
So here we know the value of tan⁡60∘\tan {60^ \circ }but we don’t know the value of tan⁡7∘,tan⁡23∘,tan⁡67∘,tan⁡83∘\tan {7^ \circ },\tan {23^ \circ },\tan {67^ \circ },\tan {83^ \circ }
Now we can convert any two of the tan⁡7∘  \tan {7^ \circ }\,\,or tan⁡23∘\tan {23^ \circ } into cot⁡θ\cot \theta by using the formula tan⁡θ=cot⁡(90−θ)\tan \theta = \cot \left( {90 - \theta } \right)
So if θ=7∘\theta = {7^ \circ }, then
tan⁡7=cot⁡(90−7) tan⁡7=cot⁡(83)  \tan 7 = \cot \left( {90 - 7} \right) \\\ \tan 7 = \cot \left( {83} \right) \\\
So if θ=23∘\theta = {23^ \circ }, then
tan⁡23=cot⁡(90−23) tan⁡23=cot⁡(67)  \tan 23 = \cot \left( {90 - 23} \right) \\\ \tan 23 = \cot \left( {67} \right) \\\
So we need to find the value of tan⁡7∘tan⁡23∘tan⁡60∘tan⁡67∘tan⁡83∘\tan {7^ \circ }\tan {23^ \circ }\tan {60^ \circ }\tan {67^ \circ }\tan {83^ \circ }
Now replace tan⁡7∘  \tan {7^ \circ }\,\,and tan⁡23∘\tan {23^ \circ } with cot⁡83∘    \cot {83^{ \circ \,}}\,\,\,and cot⁡67∘\cot {67^ \circ } respectively.
So we will get, cot⁡83∘cot⁡67∘tan⁡60∘tan⁡67∘tan⁡83∘\cot {83^ \circ }\cot {67^ \circ }\tan {60^ \circ }\tan {67^ \circ }\tan {83^ \circ }
Now after rearranging
(cot⁡83∘tan⁡83∘)tan⁡60∘(tan⁡67∘cot⁡67∘)(\cot {83^ \circ }\tan {83^ \circ })\tan {60^ \circ }(\tan {67^ \circ }\cot {67^ \circ })
We know that tan⁡θcot⁡θ=1\tan \theta \cot \theta = 1. So using we get
(cot⁡83∘tan⁡83∘)=1(\cot {83^ \circ }\tan {83^ \circ }) = 1
And (tan⁡67∘cot⁡67∘)=1(\tan {67^ \circ }\cot {67^ \circ }) = 1
Putting these value we get,
(1)×tan⁡60∘×(1)(1) \times \tan {60^ \circ } \times (1)
And we know that tan⁡60∘=3\tan {60^ \circ } = \sqrt 3
So we get the product of tan⁡7∘tan⁡23∘tan⁡60∘tan⁡67∘tan⁡83∘\tan {7^ \circ }\tan {23^ \circ }\tan {60^ \circ }\tan {67^ \circ }\tan {83^ \circ } =3= \sqrt 3

So, the correct answer is “Option B”.

Note: We should learn standard trigonometric angles of sin⁡θ,cos⁡θ &tan⁡θ\sin \theta ,\cos \theta \,\& \tan \theta .

And we should know the relations tan⁡θ.cot⁡θ=1,cos⁡θ.sec⁡θ=1,cos⁡ecθ.sin⁡θ=1\tan \theta . \cot \theta = 1,\cos \theta . \sec \theta = 1, \cos ec \theta . \sin \theta = 1.Students should also remember trigonometric formulas and identities for solving these types of problems.