Question

What is the value of \sin \left[ {{{\cot }^{ - 1}}\left\\{ {\cos \left( {{{\tan }^{ - 1}}x} \right)} \right\\}} \right]?
A) $\sqrt {\dfrac{{1 + {x^2}}}{{2 + {x^2}}}}$
B) $\sqrt {\dfrac{{2 + {x^2}}}{{1 + {x^2}}}}$
C) $\sqrt {\dfrac{{{x^2} - 2}}{{{x^2} - 1}}}$
D) $\sqrt {\dfrac{{{x^2} - 1}}{{{x^2} - 2}}}$

Answer 1

We are given a trigonometric equation and we have been asked to find its value. Assume the innermost value to be equal to theta. And then use it in the triangle to find perpendicular, base and hypotenuse. Put the theta value in the equation and find the value of the other trigonometric ratio using the triangle. Repeat this once more till you have to find the value of sin. You will get your answer.

Complete step-by-step solution:
In this question, we have been asked to find the value of a given trigonometric equation. We will use triangle method and certain inverse trigonometric identities to find the value of the given equation.
\Rightarrow \sin \left[ {{{\cot }^{ - 1}}\left\\{ {\cos \left( {{{\tan }^{ - 1}}x} \right)} \right\\}} \right]
Let ${\tan ^{ - 1}}x = \theta$
Shifting tan to the other side, we will get $x = \tan \theta$………………... (i)
Now, we also know that $\tan \theta = \dfrac{P}{B}$. Therefore, $\dfrac{P}{B} = \dfrac{x}{1}$. On comparing both the sides, we will find that $P = x,B = 1$. Using this, we will make a triangle and find the value of hypotenuse (H) using Pythagoras theorem.

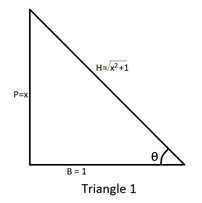
We know that ${P^2} + {B^2} = {H^2}$ (Pythagoras Theorem). Putting the values in the theorem,
$\Rightarrow {x^2} + 1 = {H^2}$
Square rooting both the sides,
$\Rightarrow \sqrt {{x^2} + 1} = H$
Take a look at Triangle 1.
Now, we will put equation (i) in the given equation.
\Rightarrow \sin \left[ {{{\cot }^{ - 1}}\left\\{ {\cos \left( {{{\tan }^{ - 1}}\left( {\tan \theta } \right)} \right)} \right\\}} \right]
We know the identity -${\tan ^{ - 1}}\left( {\tan \theta } \right) = \theta$. Using this we get,
\Rightarrow \sin \left[ {{{\cot }^{ - 1}}\left\\{ {\cos \theta } \right\\}} \right] ………….…. (ii)
Now, we can find the value of $\cos \theta$ using Triangle 1. We know that $\cos \theta = \dfrac{B}{H}$. Putting the values from the triangle,
$\Rightarrow \cos \theta = \dfrac{1}{{\sqrt {{x^2} + 1} }}$
Putting the value of $\cos \theta$ in equation (ii),
\Rightarrow \sin \left[ {{{\cot }^{ - 1}}\left\\{ {\dfrac{1}{{\sqrt {{x^2} + 1} }}} \right\\}} \right] ……………... (iii)
Now, we will again use the same method as used above to solve further.
Let ${\cot ^{ - 1}}\dfrac{1}{{\sqrt {{x^2} + 1} }} = \phi$
Shifting cot to the other side, we will get $\dfrac{1}{{\sqrt {{x^2} + 1} }} = \cot \phi$…. (iv)
We will again form a triangle. We know that $\cot \phi = \dfrac{B}{P}$. Therefore, $\dfrac{B}{P} = \dfrac{1}{{\sqrt {{x^2} + 1} }}$. On comparing both the sides, we will find that $P = \sqrt {{x^2} + 1} ,B = 1$. Using this, we will make a triangle and find the value of hypotenuse (H) using Pythagoras theorem.

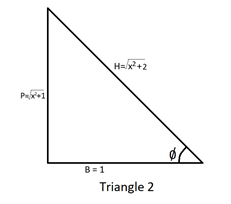
We know that ${P^2} + {B^2} = {H^2}$ (Pythagoras Theorem). Putting the values in the theorem,
$\Rightarrow {\left( {\sqrt {{x^2} + 1} } \right)^2} + 1 = {H^2}$
$\Rightarrow {x^2} + 1 + 1 = {H^2}$
Square rooting both the sides,
$\Rightarrow \sqrt {{x^2} + 2} = H$
Take a look at Triangle 2.
Now, we will put equation (iv) in (iii).
\Rightarrow \sin \left[ {{{\cot }^{ - 1}}\left\\{ {\cot \phi } \right\\}} \right]
We know the identity -${\tan ^{ - 1}}\left( {\tan \theta } \right) = \theta$. Using this we get,
$\Rightarrow \sin \phi$
Now, we can find the value of $\sin \phi$ using Triangle 2. We know that $\cos \theta = \dfrac{B}{H}$
Putting the values from the triangle,
$\Rightarrow \sin \phi = \dfrac{{\sqrt {{x^2} + 1} }}{{\sqrt {{x^2} + 2} }}$

Hence, the required answer in option A) $\sqrt {\dfrac{{1 + {x^2}}}{{2 + {x^2}}}}$

Note: We have to mind that, in mathematics, the Pythagorean Theorem, also known as Pythagoras’s theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides $a$, $b$ and $c$ often called the “Pythagorean equation”.
${a^2} + {b^2} = {c^2}$
Where $c$ represents the length of the hypotenuse and $a$, $b$ the lengths of the triangle’s other two sides.