Question
Question: What is the value of impedance of a resonant series LCR circuit?...
What is the value of impedance of a resonant series LCR circuit?
Solution
To answer this question you should know the concept of LCR circuit. It is said that an AC source of voltage V = Vmsinωt is connected to a series combination of L, C and R. Use the phasor diagram to obtain expressions for impedance of the circuit and phase angle between voltage and current. Find the condition when current will be in phase with the voltage and the circuit in this condition is called resonant circuit. Circuit in which inductance L, capacitance C and resistance R are connected in series and the circuit admits maximum current, then such circuit is called a series resonant circuit.
Complete answer:
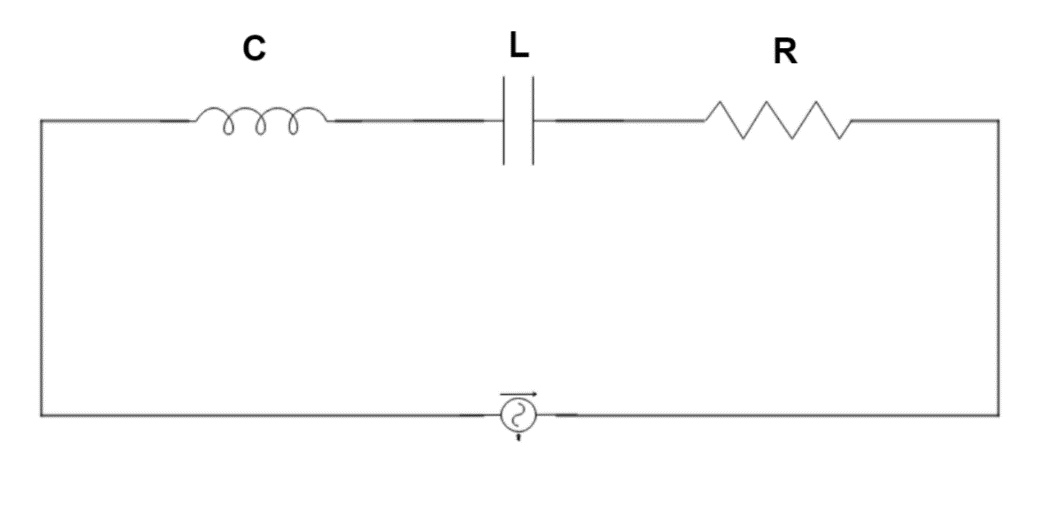
From the LCR circuit we see that the resistor, inductor and capacitance are in series. Therefore, the ac current in each element is the same at any time, having the same amplitude and phase. Let it be i=imsin(ωt+ϕ)
Where ϕ is the phase difference between the voltage across the source and the current in the circuit.
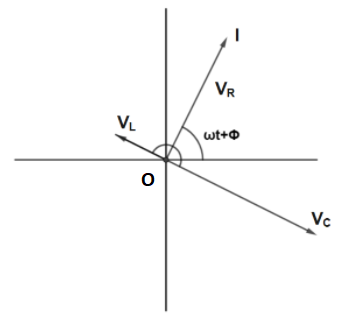
Let I be the phasor representing the current in the circuit. Further, let VL , VC , VR and Vrepresent the voltage across the inductor, resistor, capacitor and the source, respectively. we know that V, is parallel to I. VCis 2π behind I andVL is 2π ahead of I.
In an RLC circuit, impedance triangle is a right-angled triangle in which base is ohmic resistance R, perpendicular is reactance (XC - XL) and hypotenuse is impedance (Z).
VL , VC , VR and I is shown in the figure with appropriate phase-relations.
The length of these phasors or the amplitude of VL , VC , VR are:
VRm = imR , VCm = imXC , VLm = imXL
The voltage equation for the circuit can be written as
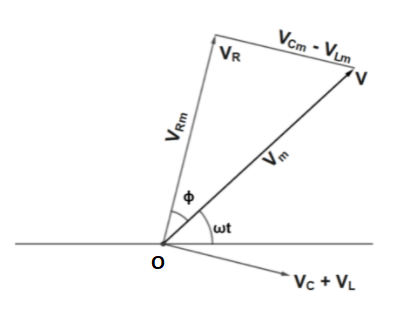
V=VL + VR + VC−−−(1)
Since VL and VC are always along the same line and in opposite directions, they can be combined into a single phasor ∣ VL + VC | which has a magnitude VCm - VLm.
∣ VL + VC | = VCm - VLm
Since V is represented as the hypotenuse of a right-triangle whose sides are V, VR and (VL + VC) the Pythagorean theorem gives:
Vm2 = VRm2 + (VCm - VLm)2
Substituting the values of VRm, VCm and VLm into the above equation, we have
⇒Vm2 = im2R2 + (imXC - imXL)2
⇒Vm2 = im2R2 + im2(XC - XL)2
⇒Vm2 = im2(R2 + (XC - XL)2)
Or,
im=R2+(XC - XL)2Vm
By the analogy to the resistance in a circuit, we introduce the impedance Z in an ac circuit:
im=ZVm
Where Z = R2+(XC - XL)2−−−(2)
From figure,
tanϕ=VRmVCm - VLm=imRim(XC - XL)
ϕ=tan−1(RXC - XL)
Condition for current and voltage are in phase:
VL = VC or XL = XC
Therefore, equation two becomes
Z = R2+0 (Because XL = XC therefore XL - XC = 0)
∴Z = R
This circuit is called a resonant circuit.
Therefore, the value of impedance of a resonant series LCR circuit is Z = R
Note:
When a condenser of capacity C charged to certain potential is connected to inductor L, energy stored in C oscillates between L and C where frequency of energy oscillations is given by f=2πLC1 . In an LCR circuit, if there is no loss of energy, then total energy in L and C at every instant will remain constant. The maximum current in an LR circuit is determined by the emf E and resistance R. The maximum charge on the capacitor in a RC circuit is determined by the emf E and capacitance C. A capacitor cannot be charged or discharged instantaneously.
