Question

What is the value of current i in the given figure?

A. $- 4\,mA$
B. $+ 2\,mA$
C. $+ 4\,mA$
D. $+ 8\,mA$

Answer 1

By applying KCL law we can solve the above problem.Kirchhoff’s Current Law often shortens as KCL, which states that the algebraic sum of all the currents entering and exiting a node must be equal to zero. In other words we can also say that the sum of current entering a node is equal to the sum of current exiting a node.

Formula Used:
$\boxed{\sum\limits_{k = 1}^n {{i_k} = 0} }$
Where, $i = \,Current$ and k varies from $k = 1,2,3, \ldots \ldots n$.

Complete step by step answer:
According to Kirchhoff’s current law, the algebraic sum of all the currents entering and exiting a node must be equal to zero. In other words we can also say that the sum of current entering a node is equal to the sum of current exiting a node.As per the question we need to calculate the value of i that is exiting from the node. For this we have to apply Kirchhoff’s current law.As given in the diagram,

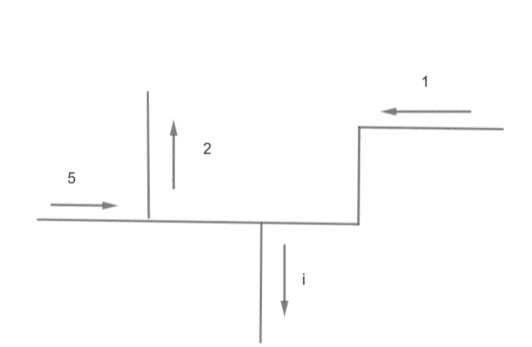
As we can see from the diagram current $5mA\,\,and\,\,1mA$ are entering current while current $2mA\,\,and\,\,i$ are exciting currents.Applying Kirchhoff Current law we can write

Method I:
$\sum\limits_{k = 1}^n {{i_k} = 0}$
Here k varies from $k = 1,2,3,4$
Now we can write,
$\sum\limits_{k = 1}^4 {{i_{1,2,3,4}}} = 0$
$\Rightarrow {i_1} + {i_2} + {i_3} + {i_4} = 0$
With the help of above diagram
${i_1} = 5mA,{i_2} = 1mA,{i_3} = 2mA,{i_4} = i$
Now putting the above value in the equation we get,
$5mA + 1mA - 2mA - i = 0$
(As ${i_3}\,\,and\,\,{i_4}$ are exiting current which flows in opposite direction)
Now,
$4mA - i = 0$
$\therefore \boxed{i = + 4mA}$

Method 2:
Entering Current=Exiting Current
$\Rightarrow 5mA + 1mA = 2mA + i$
$\Rightarrow 6mA = 2mA + i$
$\Rightarrow 6mA - 2mA = i$
$\therefore \boxed{i = + 4mA}$

Hence, the correct option is $\left( C \right)$.

Note: Always take proper sign convention when you are using method 1 to solve this kind of problem or else you will make a mistake. If in place of $- 2mA$ I will take $+ 2mA$ then my answer will be incorrect. So be careful while solving this kind of problem. It will be better for you to solve this kind of problem using method 2.