Question
Question: What is the value of $[(\cos3\theta + 2\cos5\theta + \cos7\theta) \div (\cos\theta + 2\cos3\theta + ...
What is the value of [(cos3θ+2cos5θ+cos7θ)÷(cosθ+2cos3θ+cos5θ)]+sin2θ.tan3θ?
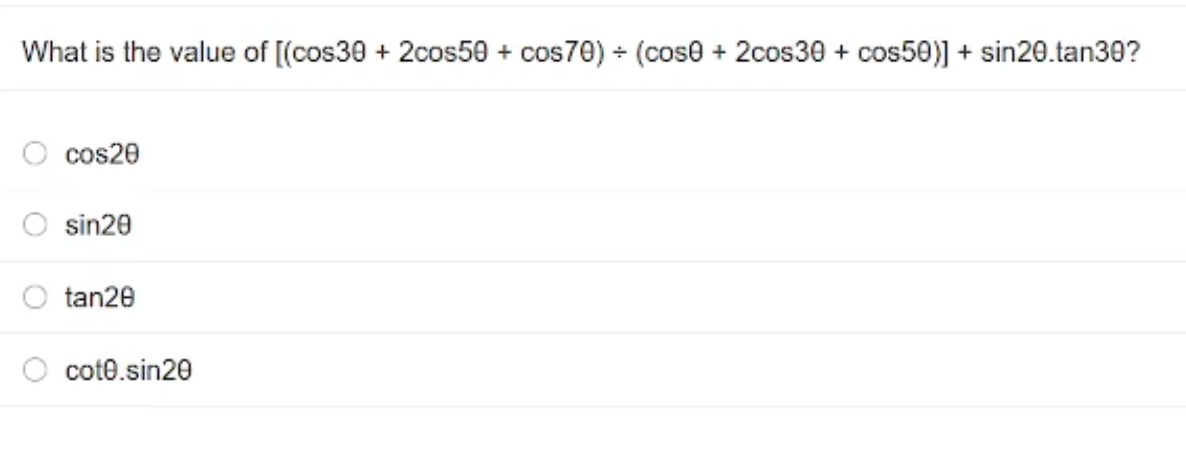
cos2θ
sin2θ
tan2θ
cotθ.sin2θ
cos2θ
Solution
The problem requires simplifying a trigonometric expression using various identities.
The given expression is: E=[cosθ+2cos3θ+cos5θcos3θ+2cos5θ+cos7θ]+sin2θ.tan3θ
Let's simplify the numerator of the first term, N=cos3θ+2cos5θ+cos7θ. We can rearrange the terms and use the sum-to-product identity cosA+cosB=2cos(2A+B)cos(2A−B): N=(cos3θ+cos7θ)+2cos5θ N=2cos(23θ+7θ)cos(27θ−3θ)+2cos5θ N=2cos5θcos2θ+2cos5θ Factor out 2cos5θ: N=2cos5θ(cos2θ+1) Now, use the identity 1+cos2θ=2cos2θ: N=2cos5θ(2cos2θ) N=4cos5θcos2θ
Next, let's simplify the denominator of the first term, D=cosθ+2cos3θ+cos5θ. Rearrange and use the sum-to-product identity: D=(cosθ+cos5θ)+2cos3θ D=2cos(2θ+5θ)cos(25θ−θ)+2cos3θ D=2cos3θcos2θ+2cos3θ Factor out 2cos3θ: D=2cos3θ(cos2θ+1) Use the identity 1+cos2θ=2cos2θ: D=2cos3θ(2cos2θ) D=4cos3θcos2θ
Now, substitute the simplified numerator and denominator back into the first term of the expression: DN=4cos3θcos2θ4cos5θcos2θ Assuming cos2θ=0, we can cancel cos2θ: DN=cos3θcos5θ
Substitute this back into the original expression: E=cos3θcos5θ+sin2θ.tan3θ Rewrite tan3θ as cos3θsin3θ: E=cos3θcos5θ+sin2θ(cos3θsin3θ) Combine the terms over a common denominator cos3θ: E=cos3θcos5θ+sin2θsin3θ
Now, use the cosine addition formula cos(A+B)=cosAcosB−sinAsinB. Let A=2θ and B=3θ, then cos(2θ+3θ)=cos5θ: cos5θ=cos2θcos3θ−sin2θsin3θ Substitute this expression for cos5θ into the numerator of E: Numerator =(cos2θcos3θ−sin2θsin3θ)+sin2θsin3θ Numerator =cos2θcos3θ
So, the expression E becomes: E=cos3θcos2θcos3θ Assuming cos3θ=0, we can cancel cos3θ: E=cos2θ
The value of the expression is cos2θ.
