Question

What is the value of $\cos \left( \dfrac{5\pi }{4} \right)$?

Answer 1

Write the argument of the given cosine function as $\left( \dfrac{5\pi }{4} \right)=\left( \pi +\dfrac{\pi }{4} \right)$ and use the fact that the cosine function is negative in the second quadrant. Use the formula $\cos \left( \pi +\theta \right)=-\cos \theta$ to simplify the expression. Use the value $\cos \left( \dfrac{\pi }{4} \right)=\dfrac{1}{\sqrt{2}}$ to get the answer. Draw the graph of the cosine function for better understanding.

Complete step by step answer:
Here we have been provided with the cosine function $\cos \left( \dfrac{5\pi }{4} \right)$ and we are asked to find its value. First we need to see some properties of the cosine function.
Now, let us draw the graph of the cosine function and see its some of the properties.

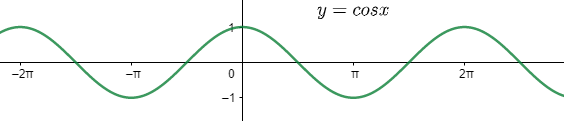
From the above graph we can see that the function is positive in the first $\left[ 0,\dfrac{\pi }{2} \right]$ and fourth $\left[ \dfrac{3\pi }{2},2\pi \right]$ quadrants and negative in the second $\left[ \dfrac{\pi }{2},\pi \right]$ and third $\left[ \pi ,\dfrac{3\pi }{2} \right]$ quadrants. We can see that the value of the cosine function lies in the range $\left[ -1,1 \right]$ and repeats its value at an interval of the angle $2\pi$ so it is a periodic function with the period $2\pi$.
Now, let us come to the question. Assuming the given expression as E we have,
$\begin{aligned} & \Rightarrow E=\cos \left( \dfrac{5\pi }{4} \right) \\\ & \Rightarrow E=\cos \left( \pi +\dfrac{\pi }{4} \right) \\\ \end{aligned}$
Clearly from the graph we can see that the value of $\cos \left( \dfrac{5\pi }{4} \right)$ will lie between the values -1 and 0 as the angle lies in the second quadrant. Also, it will follow the relation $\cos \left( \pi +\theta \right)=-\cos \theta$, so we get,
$\Rightarrow E=-\cos \left( \dfrac{\pi }{4} \right)$
We know that $\dfrac{\pi }{4}={{45}^{\circ }}$ and $\cos {{45}^{\circ }}=\dfrac{1}{\sqrt{2}}$, so we get,
$\therefore E=-\dfrac{1}{\sqrt{2}}$

Note: You must remember the graph of all the six trigonometric functions and their signs in the four quadrants. Note that sine and co – secant is positive in the first and second quadrant, tangent and co – tangent function is positive in the first and third quadrant and cosine and secant function is positive in the first and fourth quadrant. If the argument of the trigonometric function is large then we use their periodicity to find their values. Tangent and co – tangent functions have a period of $\pi$ while other four trigonometric functions have a period of $2\pi$.