Question

What is the value of $\cos \left( \dfrac{5\pi }{3} \right)$?

Answer 1

We are given a question based on finding the value of the trigonometric function with a given specific angle. We will have to first get the angle in the feasible form, so that the value of the function at that particular angle can be easily written. The angle $\dfrac{5\pi }{3}$ clearly is in the ${{4}^{th}}$ quadrant, so we will use $\cos \left( 2\pi -\theta \right)$ and solve the given trigonometric function further and we will get $\cos \left( \dfrac{\pi }{3} \right)$. We will then write the value of this function and we will have the required value of the given function.

Complete step-by-step solution:
According to the given question, we are given a trigonometric function whose value we have to find at the given angle.
The angle given to us in the question is $\dfrac{5\pi }{3}$. We know that $\dfrac{5\pi }{3}$ lies in the ${{4}^{th}}$ quadrant. And the cosecant function in the ${{4}^{th}}$ quadrant is positive, that is, in the ${{4}^{th}}$ quadrant, cosecant function has all positive values.
We will here use, $\cos \left( 2\pi -\theta \right)$, we get,
$\Rightarrow \cos \left( 2\pi -\dfrac{5\pi }{3} \right)$
Solving the above expression further, we get,
$\Rightarrow \cos \left( \dfrac{6\pi -5\pi }{3} \right)$
We now have the new expression as,
$\Rightarrow \cos \left( \dfrac{\pi }{3} \right)$
Using the special right angled triangle, we know that $\cos \theta =\dfrac{Base}{Hypotenuse}$

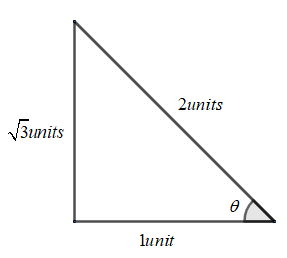
So, we have the value as,
$\Rightarrow \dfrac{1}{2}$
Therefore, the value of $\cos \left( \dfrac{5\pi }{3} \right)=\dfrac{1}{2}$.

Note: The cosecant function is an even function. Also, the values of cosecant function and the sine function are reversed. So, the values of cosecant function should be carefully written and the computation should be done in a stepwise manner.