Question
Question: What is the total current supplied by the battery to the circuit shown in the following figure? 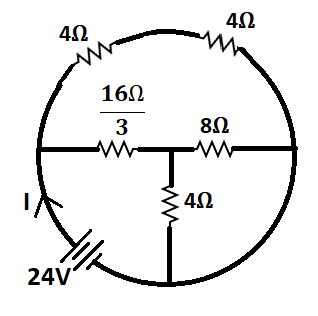
(A). 2A
(B). 4A
(C). 6A
(D). 9A
Solution
Hint : In this problem the current can be found out by finding the total resistance of the given circuit. The equivalent resistance can be found out by having basic ideas about series and parallel combinations. That is in series combination the current will remain the same whereas in parallel combination the current will be different. After finding the total resistance the current can be found out by using the formula I=RV.
Formulas used:
⇒RS1=R1+R2
⇒RP11=R11+R21
⇒V=IR
Complete step-by-step solution:
The given circuit can be redrawn as
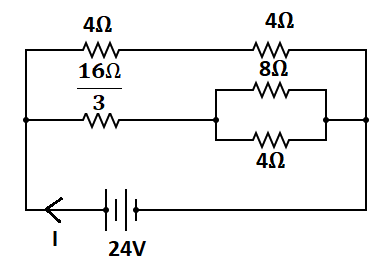
The resistors 4Ω and 4Ω are connected in series because the current remains same in these resistor, therefore equivalent resistance between these resistor is
RS1=R1+R2
Substituting the resistor values in above equation, we get
RS1=4+4
Therefore, RS1=8Ω
The resistors 8Ω and 4Ω are connected in parallel because the current different in these resistor, therefore equivalent resistance between these resistor is
RP11=R11+R21
Substituting the resistor values in above equation, we get
RP11=81+41
RP11=8×44+8
RP11=2412
RP11=21
Therefore, Rp1=2Ω
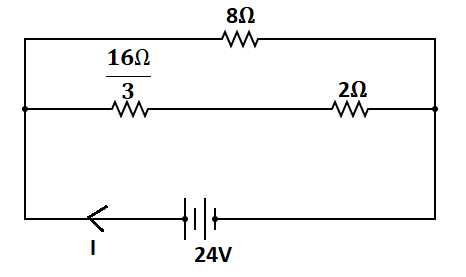
The resistors 316Ω and 2Ω are connected in series because the current remains same in these resistor, therefore equivalent resistance between these resistor is
RS2=R1+R2
Substituting the resistor values in above equation, we get
RS2=316+2
RS2=316+6
RS2=324
RS2=8Ω
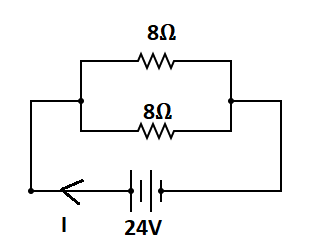
The resistors 8Ω and 8Ω are connected in parallel because the current different in these resistor, therefore equivalent resistance between these resistor is
RP21=R11+R21
Substituting the resistor values in above equation, we get
RP21=81+81
RP2=4Ω
Therefore, Total resistance R=4Ω
Then, according to the ohm’s law
V=IR
Therefore,
I=RV
I=424
I=6A
Hence, the correct option is C .That is 6A .
Note: It should be noted that the resistance of the resistor will be more when connected in series compared to that of resistor when connected in parallel. The current should be found only after finding the total resistance and the S.I unit electric current is ampere (A) .
