Question

What is the time constant of the following circuit;

A. $\dfrac{{2RC}}{3}$
B. $\dfrac{5}{3}RC$
C. $\dfrac{5}{8}RC$
D. None of the above

Answer 1

In this question, we have to find the effective resistance of the circuit. We will find the effective resistance of the circuit by simplifying the circuit, and hence considering the capacitor to be fully charged and thus acts as an open circuit . Then, by using the formula of time constant, we will find the respective solution.

Formula used:
$\tau = R \times C$
where $R$ is the total resistance of the circuit and $C$ is the capacitance of the circuit.

Complete step by step answer:
In the given question, the capacitor $C$ is to be considered as a conducting wire, hence the figure we get is,

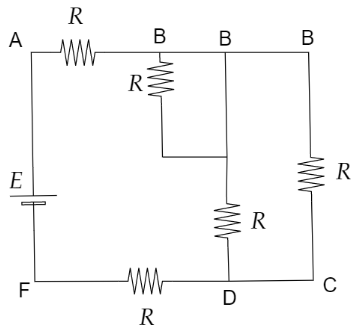
Simplifying the given circuit we get,

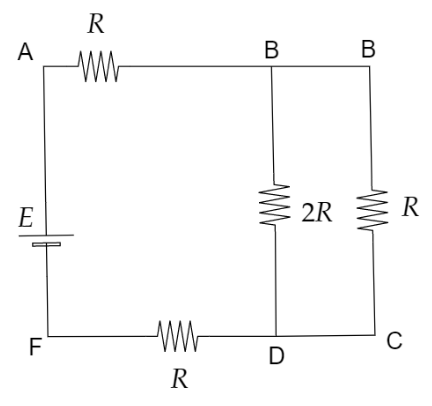
Circuits, BD and BC are in parallel connection, so the effective resistance $R'$ is given by,
$R' = \dfrac{{2R \times R}}{{2R + R}} = \dfrac{2}{3}R$
Again, by simplifying the circuit we get,

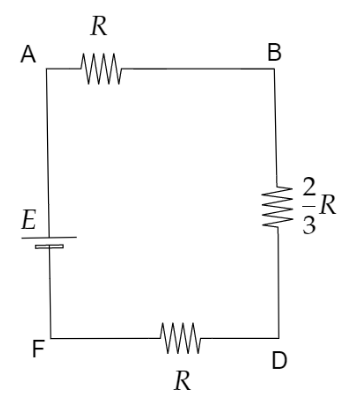
Now, the circuit AB and BD are in series, hence their effective resistance $R''$ is given by,
$R'' = \dfrac{2}{3}R + R = \dfrac{5}{3}R$
Again, the simplified circuit is,

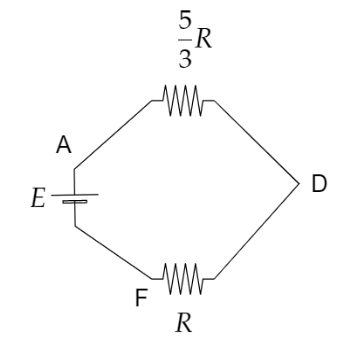
Now the effective resistance is,
$R''' = \dfrac{{\dfrac{5}{3}R \times R}}{{\dfrac{5}{3}R + R}} = \dfrac{5}{8}R$
Thus, the total resistance of the circuit is $\dfrac{5}{8}R$.

Time constant of RC Circuit is the product of capacitance of the circuit to its resistance.Let the time constant of the circuit be $\tau$.Thus,
$\tau = R \times C$
where $R$ is the total resistance of the circuit and $C$ is the capacitance of the circuit.
Substituting the values we get,
$\therefore \tau = \dfrac{5}{8}RC$

Therefore, the correct option is C.

Note: It must be noted that resistance of a circuit is to be measured by simplifying the circuit one after another. We can also use Kirchhoff’s Voltage Law to find the effective resistance. When the capacitor gets fully charged then the potentials at its both ends become the same and hence, no current flows through it.