Question
Question: What is the time constant of the C-R growth circuit shown in figure? A, 3A are the areas of the capa...
What is the time constant of the C-R growth circuit shown in figure? A, 3A are the areas of the capacitor and d is the distance between them.
(A) d7ε0A
(B) d4ε0A
(C) d2ε0A
(D) d9ε0A
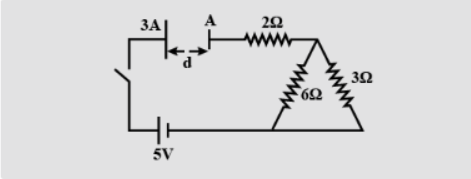
Solution
Time constant is the product of capacitance and resistance. C is given by the formula relating area A (which is the common area that is shared by the two plates), distance d between the plates and constant epsilon ε0. Resistance here means the equivalent resistance of the circuit by simplifying parallel and series combinations.
Complete step-by-step solution
In C-R growth circuits the quantity RC is called the time constant as it has the dimension of time.
t=CR
C is the capacitance while R is the equivalent resistance of the circuit.
C of the circuit is given by
C=dε0A
Even if the plates are of different areas only the area common is considered hence the capacitance is as above.
Now, we calculate the R
Resistors 3Ω and 6Ω are in parallel so
R1=3+63×6 R1=918 R1=2Ω
Now R1 is in series with 2Ω
R=R1+2 R=2+2 R=4Ω
Hence R is equal to 4Ω
Now substitute C and R in the time constant formula
t=CR t=dε0A×4 t=d4ε0A
Hence the time constant for this circuit is d4ε0A.
The correct option is B.
Note: The capacitance value depends linearly on the area of the cross section of the plates, distance between the plates and the medium between the plates while resistance depends linearly on length of the conductor, area and temperature.
