Question

What is the term symbol for Cr in ${[Cr{(CN)_6}]^{ - 4}}$ ?

Answer 1

The term symbol in quantum mechanics is an abbreviated description of the angular momentum quantum numbers in a multi-electron system. Every energy level is not only described by its configuration but also its term symbol. The term symbol usually assumes LS coupling.

Complete Step By Step Answer:
The term symbol has a form of: $^{2S + 1}{L_J}$
Where $2S + 1$ is the spin multiplicity, L is the orbital quantum number having values S, P, D, F, G, etc. and J is the total angular momentum quantum number. The value of J ranges from ${J_{\max }} - {J_{\min }}$ (max to min) . The value of ${J_{\max }} = |L + S|$ and ${J_{\min }} = |L - S|$
The spin multiplicity or the total spin angular momentum can be given as: $S = |{M_S}| = |\sum\limits_i {{m_{s,i}}} |$ for I no. of electrons. And total orbital angular momentum quantum number L can be given as: $L = |{M_L}| = |\sum\limits_i {{m_{l,i}}} |$ for I no. of electrons. If the value of L =0,1,2,3,4, etc. it corresponds to L = S,P,D,F,G, etc, respectively.
We are given the complex ${[Cr{(CN)_6}]^{ - 4}}$ . According to the spectrochemical series CN is a strong field ligand and promotes low spin complexes and pairing or electrons instead of exciting them to the higher energy level. The oxidation state of Cr in the complex is +2. The electronic configuration thus becomes:
$Cr:[Ar]3{d^4}4{s^2}$
$C{r^{ + 2}}:[Ar]3{d^4}$
Therefore, it has four electrons to be arranged in the octahedral crystal field splitting of d orbital. The splitting of d orbital for Octahedral complexes happens as below

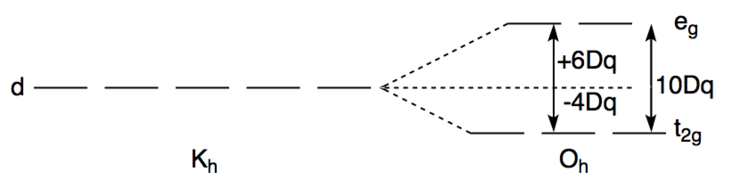
While arranging the 4 electrons in the low field pattern we will get 4 electrons in the lower ${t_{2g}}$ orbital only. ${d_{xy}}$ will have 2 electrons, ${d_{xz}},{d_{yz}}$ will have one electron each.

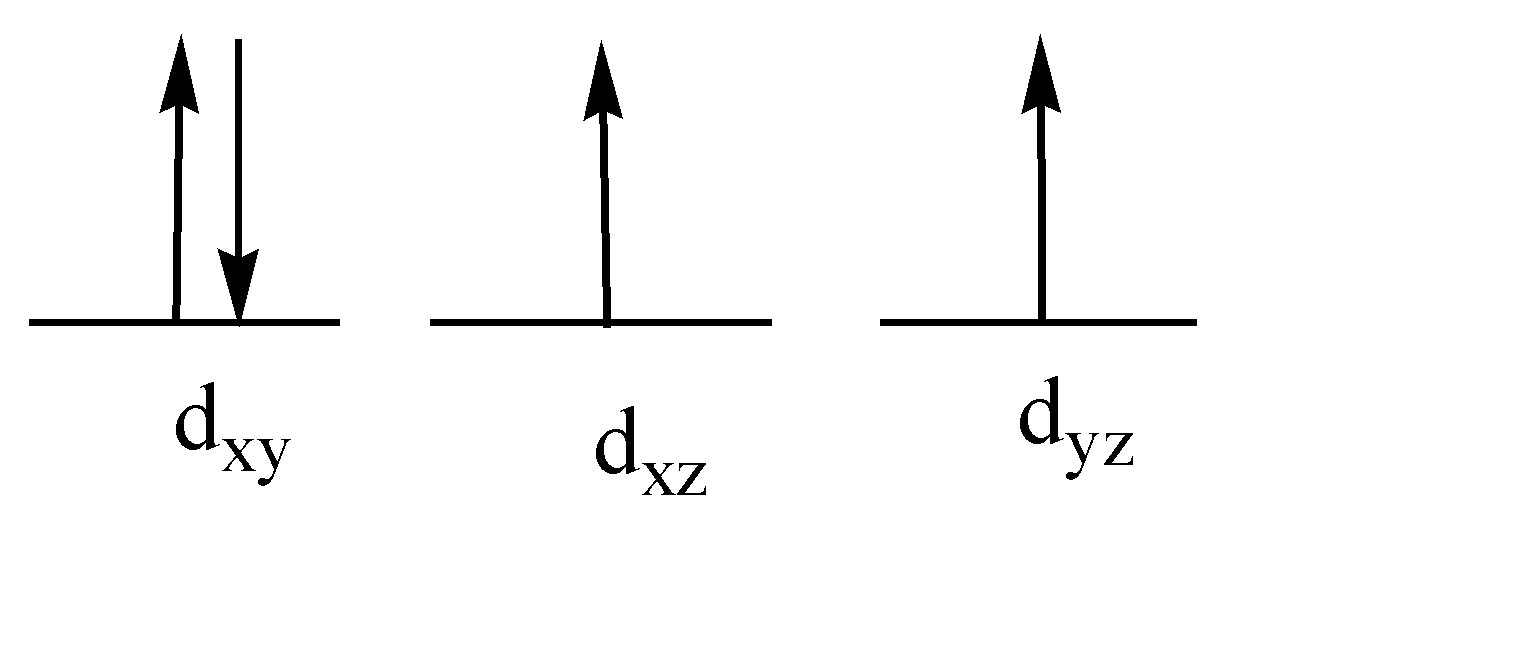
Now, since we know the electronic configuration let us find the term symbols.
The total spin angular momentum can be given as: $S = |{M_S}| = |\sum\limits_i {{m_{s,i}}} |$
For the given configuration of electrons the value of $S = \dfrac{1}{2} - \dfrac{1}{2} + \dfrac{1}{2} + \dfrac{1}{2} = 1$
The spin multiplicity will be equal to ${S_m} = 2S + 1 = 2(1) + 1 = 3$ . Spin multiplicity = 3 indicates Triplet state.
The value of total orbital angular momentum quantum number L can be given as: $L = |{M_L}| = |\sum\limits_i {{m_{l,i}}} |$
The doubly occupied orbital will have a ${m_l} = - 2$ and singly occupied orbitals will have ${m_l} = - 1,0$ respectively. The total angular momentum quantum number L will be: $L = | - 2 - 1 + 0| = | - 5| = 5 \to H$
The term symbol until now can be written as $^3H$
The value of J will be from ${J_{\max }} = |L + S|$ to ${J_{\min }} = |L - S|$ i.e. from ${J_{\min }} = |5 - 1| = 4$ to ${J_{\max }} = |5 + 1| = 6$ . Therefore, the value of J will be $J = 4,5,6$
Substituting the values to find the term symbols for ${[Cr{(CN)_6}]^{ - 4}}$ : $^3{H_4}{,^3}{H_5}{,^3}{H_6}$
This is the required answer.

Note:
If we are asked the ground state term symbol, the value of J will be ${J_{\min }} = |L - S|$ for less than half filled orbitals and ${J_{\max }} = |L + S|$ for more than half filled orbitals. In this case the orbital is less than half filled, hence the value of J will be ${J_{\min }} = |5 - 1| = 4$ and the ground state term symbol will be $^3{H_4}$ .