Solveeit Logo
Login

Question

Question: What is the standard form of the equation of a circle with center (0,0) and whose radius is 5?...

What is the standard form of the equation of a circle with center (0,0) and whose radius is 5?

Explanation

Solution

We need to find the standard form of the equation of a circle. We solve the given question using the general form of the circle given by (x−a)2+(y−b)2=r2{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}} . We substitute the center(a,b)\left( a,b \right) as (0,0)\left( 0,0 \right) and radius(r)\left( r \right) as 55 to get the desired result.

Complete step by step solution:
We are asked to find the standard form of the equation of a circle of radius 5. We will be solving the given question by substituting the centre(a,b)\left( a,b \right) as (0,0)\left( 0,0 \right) and radius(r)\left( r \right) as 55 in the equation (x−a)2+(y−b)2=r2{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}
A circle is a two-dimensional figure in which a set of points are at a fixed distance from a center. The diameter is a line that divides a circle into two halves and is twice the radius of the circle.
The general equation of the equation of a circle with center(a,b)\left( a,b \right) and radius(r)\left( r \right) is given by
⇒(x−a)2+(y−b)2=r2\Rightarrow {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}
According to the question,
The center of the circle is given as (0,0)\left( 0,0 \right)
The radius of the circle is given as 55
⇒r=5\Rightarrow r=5
Substituting the values of center and radius in the general equation of a circle, we get,
⇒(x−0)2+(y−0)2=52\Rightarrow {{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}={{5}^{2}}
Simplifying the above equation, we get,
⇒x2+y2=25\Rightarrow {{x}^{2}}+{{y}^{2}}=25
The circle with center(0,0)\left( 0,0 \right)and radius 5 can be constructed as follows,
1. Mark a single point on a sheet of paper as the center of the circle.
2.Draw a line segment OP of length 5 from the centre of the circle P for the radius.
3. Using the ruler, mark points of length 5 from the center of the circle in all directions.
4. Join all the points to construct a circle.
The diagram of the circle is represented as follows,

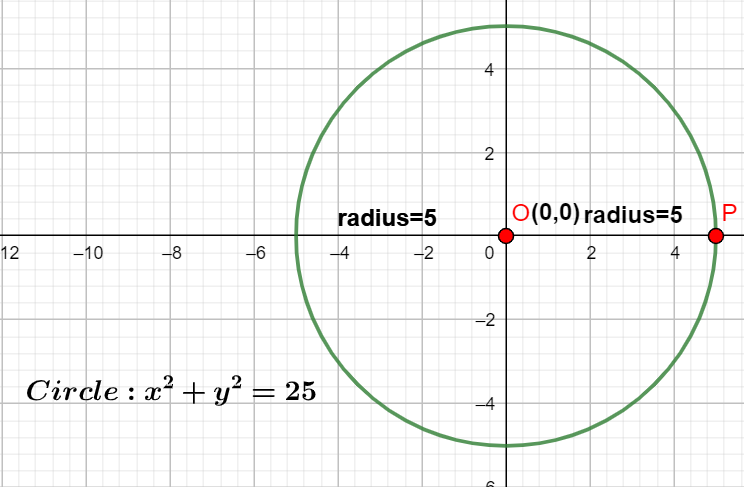
∴\therefore The standard form of the equation of a circle with center (0,0) and radius 5 is x2+y2=25{{x}^{2}}+{{y}^{2}}=25

Note: We should always make sure that all the points must be equidistant from the center while constructing a circle. We need to precisely measure the length of the radius of a circle with a ruler before marking it on the plane.