Question

What is the standard form of the equation of a circle with centre (-3,-4) and a radius of 3?

Answer 1

We know that for a circle with centre (a,b) and radius r, the standard equation of such a circle is
${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$
According to the problem, we should substitute a = -3, b=-4 and r = 3, to get the required equation.

Complete step by step solution:
Let us assume a circle with centre C with coordinates (a,b) and radius r.

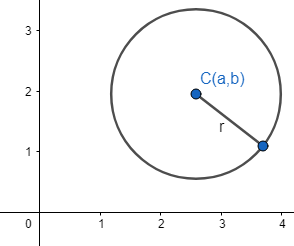
We know that the standard form of this circle is
${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$
In our given problem, we are given that the centre is (-3,-4).
Thus, on comparing with the standard form, we get
$\begin{aligned} & a=-3 \\\ & b=-4 \\\ \end{aligned}$
Substituting the values of a and b, in the standard form, we get
${{\left( x-\left( -3 \right) \right)}^{2}}+{{\left( y-\left( -4 \right) \right)}^{2}}={{r}^{2}}$
We can further simplify this equation as,
${{\left( x+3 \right)}^{2}}+{{\left( y+4 \right)}^{2}}={{r}^{2}}$
Now, we are also given that the radius of the circle is 3.
So, substituting r = 3 in the above equation, we get
${{\left( x+3 \right)}^{2}}+{{\left( y+4 \right)}^{2}}={{\left( 3 \right)}^{2}}$
We can simplify this equation as
${{\left( x+3 \right)}^{2}}+{{\left( y+4 \right)}^{2}}=9$
This is the required standard form for the circle with centre (-3,-4) and radius of 4 units.

Note: We can further simplify this standard form by using the identity ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$ , but then we will get the general equation and not the standard form.
We must remember that ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$ is the standard form of the circle with centre at origin (0,0). So, we should not use this equation in this problem.