Question

What is the standard equation of a circle?

Answer 1

We will first understand the definition of a circle and see their properties. We will assume the radius and the center of the circle is constant because center and radius are fixed or constant for a circle. We will use the distance formula between two points to find the radius.

Complete step by step answer:
Definition of circle: A circle is made up of all points on a plane that are evenly separated from a fixed point. The fixed point is known as the circle's center. The radius of the circle is the distance between the center and any point on the circumference.
We will assume the radius of the circle be R and the center of the circle be the point C(h,k).

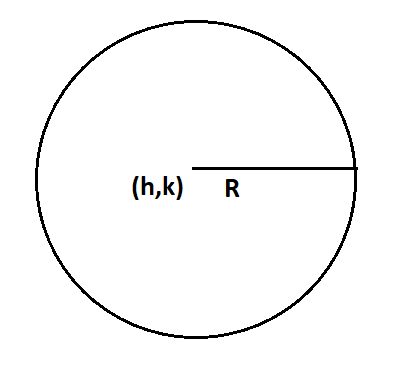
We have to find the equation of the circle
We will let a point P(x,y) on the circumference of the circle.
We know that distance between two point is ${{D}} = \sqrt {{{\left( {{{{x}}_{{2}}}-{{{x}}_{{1}}}} \right)}^{{2}}} + {{({{{y}}_{{2}}}-{{{y}}_{{1}}})}^{{2}}}}$
Where D is the distance between the points $a({{{x}}_{{1}}},{{{y}}_{{1}}})$ and $b({{{x}}_{{2}}},{{{y}}_{{2}}})$ .
Now, we will substitute the D as equals to radius, a as centre and b as any point on the circumference.
When we will put the values, we get
$\Rightarrow \sqrt {{{\left( {x - h} \right)}^{2\;}} + {{\left( {y - k} \right)}^2}} = R$
We will square both sides, we get
$\Rightarrow {\left( {x - h} \right)^{2\;}} + {\left( {y - k} \right)^2} = {R^2}$
Hence, we get standard equation of the circle is ${\left( {x - h} \right)^{2\;}} + {\left( {y - k} \right)^2} = {R^2}$

Note:
The general form of the equation of circle can be given as ${x^{2\;}} + \;{y^{2\;}} + \;2gx\; + \;2fy\; + \;c\; = \;0$ , where centre is given by $m\;( - g, - f)$ and the radius is given by ${R^2}\; = \;{g^{2\;}} + \;{f^2} - \;c$ . we should also be familiar with the formulas of circumference, area etc.