Question

What is the slope of the line $y=2$?

Answer 1

The given line is y=2, there can be many ways to find the slope of a given line. The three main and basic ways to do it are - the basic definition of slope i.e., it is the tangent of the angle it makes with the positive x-axis, it is the change in values of y and x given by derivative $\dfrac{dy}{dx}$ and from the standard form of a line y=mx+c. So we will use the first method and verify using the second one.

Complete step by step solution:
So, we have to find the slope of line y=2.
Using definition, slope is tangent of the angle it makes with the positive x-axis, we can express it as
$m=\tan \theta =\dfrac{\Delta y}{\Delta x}$
So, the slope is the ratio of the rise (vertical change) to run (horizontal change). So, we can say
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Let us first plot the graph for y=2. It will be a horizontal line passing through points with y-coordinate as 2.

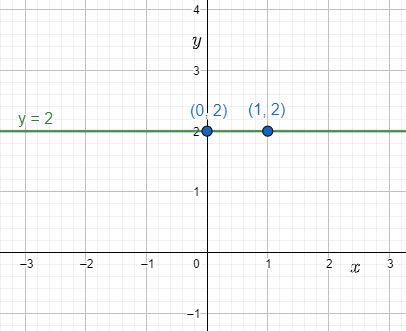
It can be easily seen that $\left( 0,2 \right)$ and $\left( 1,2 \right)$ lies on the line. Thus, the slope is

& m=\dfrac{2-2}{1-0} \\\ & m=0 \\\ \end{aligned}$$ In our second method, we are going to use $$\dfrac{dy}{dx}$$ to verify. Now let's change the line in another form, $$f\left( x \right)=y=2$$ So, we can say that $m=\dfrac{f(x+\Delta x)-f(x)}{\Delta x}$ Let us take the delta-x approaching zero (why?) (because if we look at this value, for the case of a curve, this represents the slope of a secant. As we decrease delta-x our approximation becomes more and more accurate i.e., the secant starts becoming the tangent) So, the expression turns out to be $\displaystyle \lim_{\Delta x \to \infty} \dfrac{f(x+\Delta x)-f(x)}{\Delta x}$ Which is nothing but $$\dfrac{dy}{dx}$$. $$\begin{aligned} & m=\dfrac{dy}{dx} \\\ & m=\dfrac{d}{dx}\left( 2 \right) \\\ & m=0 \\\ \end{aligned}$$ Hence, the slope of line y=2 is 0. **Note:** We can conclude that differentiation of a curve at a particular point represents its slope at that point, (and in the case of a straight line it is the same for every point). Also, note that the given line is parallel to the x-axis so we directly conclude without solving that its slope will be 0. Using third method, we are directly using the slope form of the line $$y=mx+c$$ Where “m” represents the slope of the line and “c” represents the intercept it makes with the y-axis. So, converting our line in this form, we get By comparison, we can see that slope is $$0$$.