Question

What is the slope of the line $3x+5y=15$

Answer 1

This type of question is based on the concept of slope-intercept form of a line. The equation of a line in slope-intercept form is given by, $y=mx+c$ where $m$ is the slope and $c$ is the y-intercept of the line. By rearranging the given equation of line in slope-intercept form we are able to find out the slope of the line.

Complete step by step solution:
Now, consider the equation of the given line which is $3x+5y=15$
Rearrange $3x+5y=15$ in slope intercept form.
Move all the terms not containing y to the right side of the equation.
On Subtracting $3x$ from both the sides, we get,
$\Rightarrow 5y=15-3x$
Now, dividing both sides by 5, we can write,
$\Rightarrow \dfrac{5y}{y}=\dfrac{15}{5}-\dfrac{3}{5}x$
$\Rightarrow y=3-\left( \dfrac{3}{5} \right)x$
We can rewrite the above equation as,
$\Rightarrow y=-\left( \dfrac{3}{5} \right)x+3$
This is nothing but the slope-intercept form of the given equation of line. So, we get,
$\Rightarrow m=-\dfrac{3}{5}$And $c=3$
The slope of the line is the value of $m$ and the y-intercept is the value of $c$.
Hence, Slope =$m=-\dfrac{3}{5}$and y-intercept = $c=3$
Therefore the slope of the equation of line $3x+5y=15$ is $-\dfrac{3}{5}$.

Note: Here, in case of finding slope of the equation of line $3x+5y=15$ instead of using slope-intercept form students can use graphical method as follows,
First we to draw the graph of the equation of line $3x+5y=15$ which is,

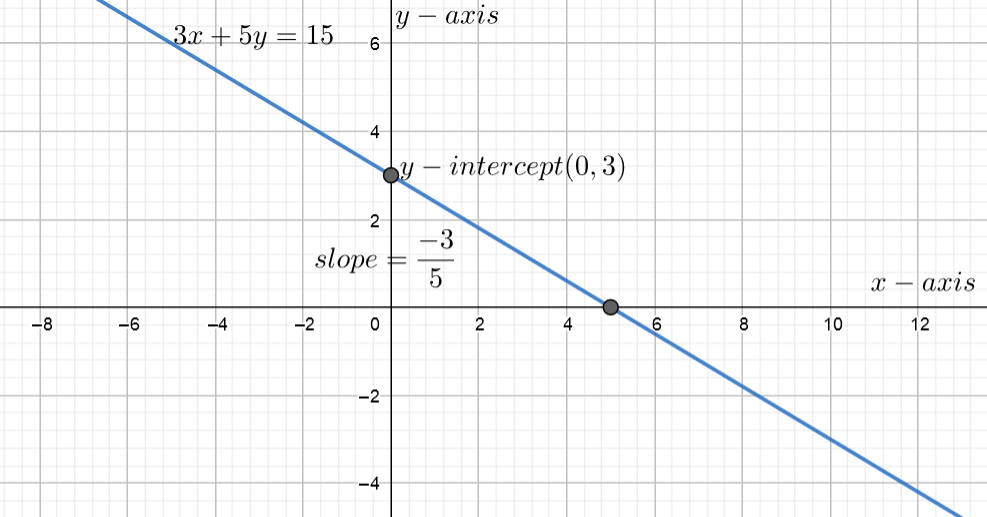
Here, $A(0,3)$ and $B(5,0)$ are two points on the given line.
So that, ${{x}_{1}}=0,{{y}_{1}}=3,{{x}_{2}}=5\And {{y}_{2}}=0$
Hence, slope of the corresponding line can be given by,
$\Rightarrow m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
$\Rightarrow m=\dfrac{0-3}{5-0}$
$\Rightarrow m=\dfrac{-3}{5}$
$\Rightarrow m=-\dfrac{3}{5}$
Therefore the slope of the equation of line $3x+5y=15$ is $-\dfrac{3}{5}$.