Question

What is the slope of intercept for $y = \dfrac{1}{2}x - 3$ and how do you graph it?

Answer 1

we need to find the slope of $y = \dfrac{1}{2}x - 3$ and then determine a way to graph it. The first step to do this is by finding the general equation for the slope intercept form, then compare the given equation with the general equation to find the slope of the equation. Then, the last step is to substitute the value of one of the variables in the equation to get the corresponding value to find the graph.

Complete Step By Step solution:
The given equation is $y = \dfrac{1}{2}x - 3$.
The general form for the slope intercept form is $y = mx + c$. Here, m is the slope and c is the y intercept.
Now compare the equation $y = mx + c$ and $y = \dfrac{1}{2}x - 3$. From the two equations the slope of the equation $y = \dfrac{1}{2}x - 3$ is $m = \dfrac{1}{2}$.
Since, the value of the y intercept is $- 3$ where y intercept is the point where the line cuts the y axis.
The next step is to find the x intercept. To obtain the x intercept, substitute $y = 0$ in the equation $y = \dfrac{1}{2}x - 3$.

$$0 = \dfrac{1}{2}x - 3 \\\ x = \dfrac{{3 \times 2}}{1} \\\ \Rightarrow x = 6 \\\$$

Then, mark the point $\left( {0, - 3} \right)$ and $\left( {6,0} \right)$ on the graph and join the line to make the graph.
The graph is shown in figure below.

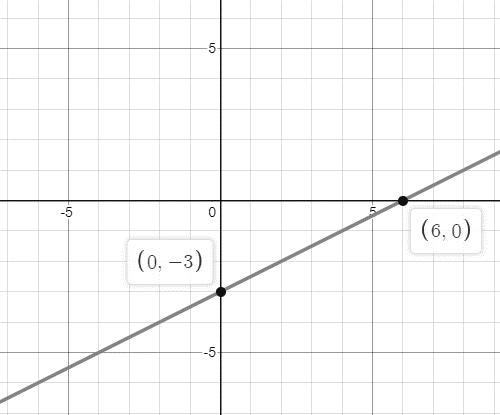
Thus, the slope of the line and the graph for the line is obtained.

Note:
The slope of the line is the plane that has x and y coordinates and is defined to change in the value of the y coordinate with respect to change in the value of the x coordinate. The general form for the slope of line $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$. If the two lines have equal slope then the two lines will never intersect, if the two lines have different slopes then they will intersect.