Solveeit Logo
Login

Question

Question: What is the slope and y-intercept of the line \(y=-2x+8\)?...

What is the slope and y-intercept of the line y=−2x+8y=-2x+8?

Explanation

Solution

For solving this question you should know about the slope of a line and the y-intercept of a line. If the point is given at x-axis, then we will see the change at that axis. If the change occurs there, then there will be a slope which we will count by calculations but if there is no change or Δx=0\Delta x=0, then it has no slope and it never cuts the y-axis also. And if it has a slope, then use it to find them.

Complete step by step solution:
According to our question it is asked of us to find the slope and y-intercept of the line y=−2x+8y=-2x+8. If we find the y-intercept then it is found where the line in question crosses the y-axis (vertical axis), or when our x in a coordinate point is 0, such as (0, y) the slope if found by the change in y/change in x.
The slope intercept form is y=mx+by=mx+b where m is the slope and b is the y-intercept. If we have to find the slope, take any two points along the line or two given. For example, (3, 6) and (5, 7). The change in y is going to be y2−y1{{y}_{2}}-{{y}_{1}} or in case of 7 - 6, which is equal to one. Then we calculate our change in x, which is done in a same way but with x variables: x2−x1{{x}_{2}}-{{x}_{1}} or in case of 5 - 3, it will be equal to 2.
Therefore, for example, our slope will be ΔyΔx\dfrac{\Delta y}{\Delta x} and here,
Δy=y2−y1=1\Delta y={{y}_{2}}-{{y}_{1}}=1
And,
Δx=x2−x1=2\Delta x={{x}_{2}}-{{x}_{1}}=2
So, the slope is 12\dfrac{1}{2}.
But here the equation is given in the form of y=mx+cy=mx+c and here the slope of the line is,
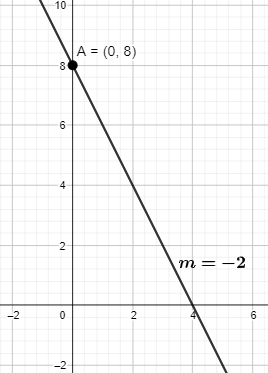
y=−2(x)+8 ⇒m=−2 \begin{aligned} & y=-2\left( x \right)+8 \\\ & \Rightarrow m=-2 \\\ \end{aligned}
So, the slope is -2.
And y-intercept refers to the value when xx equals to zero, then,
y=−2(0)+8 y=0+8 y=8 \begin{aligned} & y=-2\left( 0 \right)+8 \\\ & y=0+8 \\\ & y=8 \\\ \end{aligned}
So, the slope is -2 and y-intercept is (0, 8).

Note: The y-intercept of any line occurs only when x intersects y. And if that is not intersecting or cutting to that then, it will not have any y-intercepts there. And if the change in x values of any equation of line is equal to zero then the slope of that line always has undefined values.