Question

What is the slope and intercept of $3x + y = 5$?

Answer 1

Let $m$ be the slope of a line and $c$ its intercept on y-axis. Then the equation of this straight line is written as $y = mx + c$ and this form is known as slope intercept form. So by comparing the given expression with slope intercept form we can easily find the slope and intercept.
Formula used:
Slope intercept form (standard form of equation of a straight line)
$y = mx + c$; In which m is the slope of line and $c$ is the intercept on y-axis

Complete step-by-step solution:
Step 1: Conversion of given expression ($3x + y = 5$) into slope intercept form
We know that slope intercept form is given by
$y = mx + c$...........................Equation-1
Where m is the slope and c is the intercept on y-axis
Now by rearranging terms we get
$3x + y = 5$
$- y = 3x - 5$
Step 2: Multiplying left hand side and right hand side with $- 1$, we get
$- y = 3x - 5$
$( - 1) \times ( - y) = ( - 1) \times (3x - 5)$
Multiplying $( - 1)$ with $( - y)$, we get
$y = ( - 1) \times (3x - 5)$
Multiplying $( - 1)$with$(3x - 5)$, we get
$y = - 3x + 5$..............................Equation-2
Step 3: comparing equation-1 and equation-2
Now we converted equation-2 in slope intercept form i.e. $y = mx + c$
After comparing both equations with each other we get,
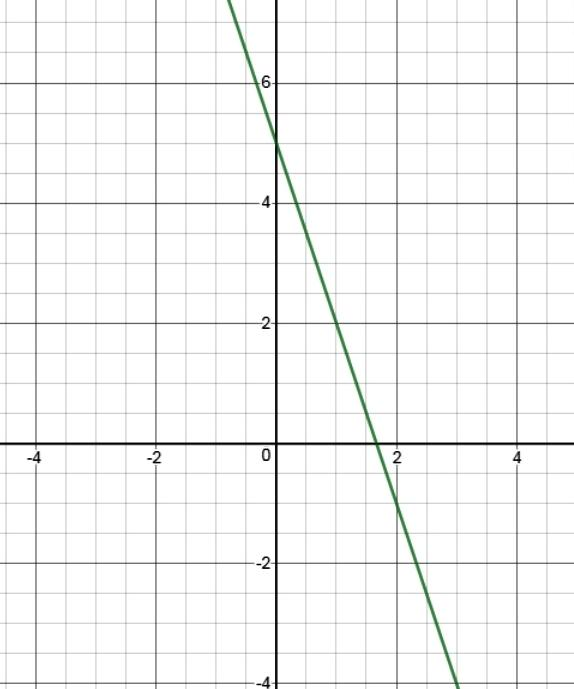
$m = - 3$& $c = 5$
Hence, slope is equal to $- 3$ and intercept on y-axis is equal to $5$

Additional information: We may also have an equation in general form, $ax + by + c = 0$ which also represents a straight line.

1. Slope of this line = - \dfrac{a}{b}$$$$ = $- \dfrac{{coeff.of(x)}}{{coeff.of(y)}}$
2. Intercept by this line on x-axis$= - \dfrac{c}{a}$ and intercept by this line on y-axis$= - \dfrac{c}{b}$

Note: Here we should have knowledge of few equations following as:

Equation of a line parallel to x-axis at a distance $a$is $y = a$or $y = - a$
Equation of x-axis is $y = 0$
Equation of line parallel to y-axis at a distance $b$is $x = b$or $x = - b$
Equation of y-axis is $x = 0$