Question

What is the slope and intercept form of$y=6x+3$?

Answer 1

In the given question, we have been an equation in two variables. Firstly, we figure out what formula should be used. Here, we know that the given line equation is in the form of slope-intercept form. In the slope-intercept form equation $y=mx+c$, where ‘m’ is the slope and ‘c’ is the y=intercept. The intercepts are the points at which the line cuts the x-axis and y-axis by putting $y=0$ and $x=0$ respectively. To find out the x-intercept and y-intercept, the equation is $\dfrac{x}{a}+\dfrac{y}{b}=1$, where $a$ is the x-intercept and $b$ is the y-intercept.

Complete step by step answer:
Let us solve the question:
We have to find the slope and intercepts of the line given by the equation
$y=6x+3$.
We will use the slope-intercept formula to find the slope of the line.
The formula for slope-intercept form is $y=mx+c$.
We can see that the given equation is already in the form of $y=mx+c$.
$m=6$and $y=3$.
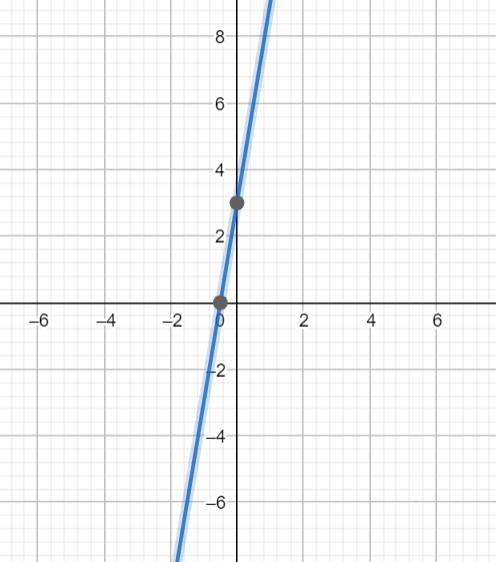
Thus, the slope of the given line is $6$ and the y-intercept is $3$.
Now we rewrite the given equation in the form $\dfrac{x}{a}+\dfrac{y}{b}=1$.
$y=6x+3$
$\Rightarrow -6x+y=3$
Dividing the above equation with ‘3’ on both sides
$\Rightarrow \dfrac{-6}{3}x+\dfrac{y}{3}=\dfrac{3}{3}$
Then we obtain,
$\Rightarrow \dfrac{x}{\left( -\dfrac{3}{6} \right)}+\dfrac{y}{\left( 3 \right)}=1$
$\Rightarrow \dfrac{x}{\left( -\dfrac{1}{2} \right)}+\dfrac{y}{\left( 3 \right)}=1$
Therefore, we get x-intercept $a=-\dfrac{1}{2}$ and y-intercept $b=3$.
Hence, the slope of the line $y=6x+3$ is $6$ and it cuts the x-axis at the point $\left( -\dfrac{1}{2},0 \right)$and y-axis at the point $(0,3)$.

Note: If a line is positioned from the bottom left to upper right, then the slope is a positive slope. If a line is positioned from the bottom left to upper right, then the slope is a positive slope. We can also find the x intercept of the line by putting $y=0$ as when the line is cutting the x-axis the value of y is 0. Similarly, we can also find the y-intercept of the line by putting $x=0$ in the equation.