Question
Question: What is the slope and intercept for \( y = \dfrac{1}{4}x \) and how would you graph it?...
What is the slope and intercept for y=41x and how would you graph it?
Solution
Hint : In order to determine the slope and intercept to the above equation first rewrite the equation as y=41x and compare with the slope-intercept form y=mx+c , m is the slope and c is the y-intercept.
Complete step-by-step answer :
We are given a linear equation in two variables xandy i.e y=41x
To determine the slope and intercept of the above equation comparing it with the slope-intercept form y=mx+c
Where, m is the slope and c is the y-intercept.
Rewriting our equation
y=41x+0 comparing with slope-intercept form y=mx+c
So
m=41 c=0
Now graph the equation, we are jumping on the cartesian plane.
There is one most important property of a plane that graphs the equation of form ax+by+c=0 is always a straight line.
Graph of equation having y-intercept as (0,0) with slope m=41
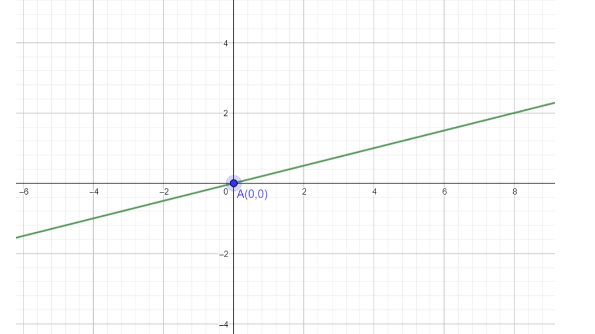
Hence, we’ve successfully plotted our graph of y=41x+0
Therefore, the slope and intercept to the expression y=41x is equal to 41and0 respectively.
Note : 1. Cartesian Plane: A Cartesian Plane is given its name by the French mathematician Rene Descartes, who first used this plane in the field of mathematics. It is defined as the two mutually perpendicular number lines, the one which is horizontal is given the name x-axis and the one which is vertical is known as y-axis. With the help of these axes we can plot any point on this cartesian plane with the help of an ordered pair of numbers.
2.Slope-Intercept Form= y=mx+c
