Question

What is the slope and intercept for $y = \dfrac{1}{4}x + 2$ and how would you graph it?

Answer 1

Hint : In this question, we are given a linear equation in terms of two variable quantities namely x and y. We can express a linear equation in several forms and one such way is slope-intercept form where we express y in terms of the slope, x and the y-intercept. On comparing this equation with that form, we will find the slope and the y-intercept. To find the x-intercept, we will put y equal to zero in the given equation.

Complete step-by-step answer :
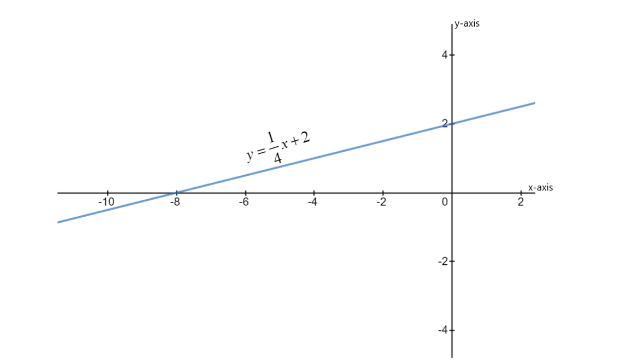
The equation of the line is $y = \dfrac{1}{4}x + 2$
We know that the slope-intercept form of the equation of the line is $y = mx + c$
On comparing the above two equations, we get that the slope of the line is $\dfrac{1}{4}$ and the y-intercept of this line is $2$ .
Now, we know the slope of the line and one point lying on this line, we can find one more point by putting the value of y equal to 0 –
When $y = 0$
$0 = \dfrac{1}{4}x + 2 \\\ \Rightarrow \dfrac{1}{4}x = - 2 \\\ \Rightarrow x = - 8 \;$
The line cuts the x-axis at the point $( - 8,0)$ .
We can trace the line of the equation $y = \dfrac{1}{4}x + 2$ by joining these two points and then extending the obtained line away in the opposite directions.

Note : To plot the graph of a straight line we must know the coordinates of at least two points lying on the line so we can put random values of one variable and get the corresponding values of the other variable. Put the value of both x and y zero one by one and then find the value of another variable from the equation of the line.