Question

What is the slope and intercept for $2x + 3y = 9$ and how would you graph it?

Answer 1

Hint : Change of the form of equation will give us the slope of the line $2x + 3y = 9$ . We have to change it to the form $y = mx + c$ to find the slope $m$ . Then, as we know that there are two kinds of intercepts which are $x$ -intercept and $y$ -intercept. So, $x$ -intercept is the point where the line intersects the $x$ -axis and $y$ -intercept is the point where the line intersects the $y$ -axis. So, to calculate the intercepts, we will put $x$ and $y$ as zero one by one. Lastly, to draw a graph, we will use the coordinates of the intercepts and draw the line.

Complete step-by-step answer :
(i)
We are given the line equation:
$2x + 3y = 9$
In order to find the slope of the line we will have to convert this equation into slope-intercept form i.e.,
$y = mx + c$
Therefore, we will subtract $2x$ from both the sides of the equation:
$2x + 3y - 2x = 9 - 2x$
On simplifying, it will become:
$3y = 9 - 2x$
Now, we will divide both the sides of the equation by $3$ :
$\dfrac{{3y}}{3} = \dfrac{{9 - 2x}}{3}$
On simplifying, we will get:
$y = \dfrac{9}{3} - \dfrac{{2x}}{3} \\\ y = 3 - \dfrac{2}{3}x \\\$
Writing the equation in slope intercept form, it will look like:
$y = - \dfrac{2}{3}x + 3$
Now, since we have our equation in the slope-intercept form, we will compare the above equation with $y = mx + c$ to find the value of $m$ .
As we can see that the coefficient of $x$ is $m$ , in our equation the coefficient of $x$ is $- \dfrac{2}{3}$ .
i.e.,
$m = - \dfrac{2}{3}$
Therefore, the slope of the equation $2x + 3y = 9$ is $- \dfrac{2}{3}$
(ii)
Now, as we know that $x$ -intercept is the point where the line crosses the $x$ -axis and we also know that on $x$ -axis, $y = 0$ . Therefore, to find the $x$ -intercept, we will put $y$ as $0$ in the equation of line given to us. Therefore,
$2x + 3\left( 0 \right) = 9 \\\ 2x = 9 \\\ x = \dfrac{9}{2} \\\$
Therefore, the $x$ -intercept of the equation $2x + 3y = 9$ is $\dfrac{9}{2}$
(iii)
Similar to $x$ -intercept, $y$ -intercept is the point where the line crosses the $y$ -axis and we also know that on $y$ -axis, $x$ =0. Therefore, to find $y$ -intercept, we will put $x$ as $0$ in the equation of the line given to us. Therefore,
$2\left( 0 \right) + 3y = 9 \\\ 3y = 9 \\\ y = \dfrac{9}{3} \\\ y = 3 \\\$
Therefore, the $y$ -intercept of the equation $2x + 3y = 9$ is $3$
(iv)
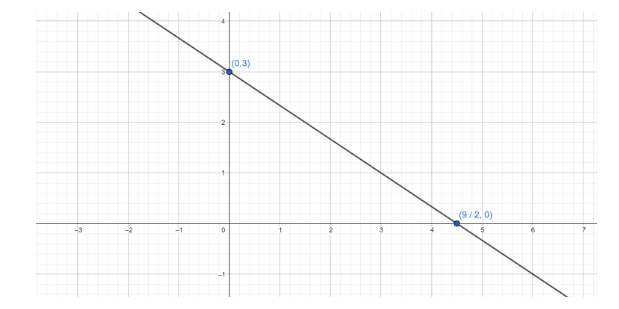
Now, to draw a graph we need two points which lie on the line. As we have calculated both the intercepts, we can say that the line crosses the $x$ -axis when $x = \dfrac{9}{2}$ as the $x$ -intercept of the given line is $\dfrac{9}{2}$ and we also know that on the $x$ -axis, $y = 0$ . So, we have a point $\left( {\dfrac{9}{2},0} \right)$ which lies on the line.
Similarly, the line crosses the $y$ -axis when $y = 3$ as the $y$ -intercept of the given line is $3$ and we also know that on the $y$ -axis, $x = 0$ . So, we have another point which lies on the line as $\left( {0,3} \right)$ .
Marking these two points on a graph and then joining the points through a line will give us the graphical representation of the line $2x + 3y = 9$ .

Note : A line parallel to $x$ -axis, does not intersect the $x$ -axis at any finite distance and hence, we cannot get any finite $x$ -intercept of such a line. Slope of such a line is $0$ . Similarly, lines parallel to the $y$ -axis, do not intersect $y$ -axis at any finite distance and hence, we cannot get any finite $y$ -intercept of such a line. Slope of such a line is $\infty$ .
In an equation of the form $y = mx + c$ , $m$ represents the slope of the line and $c$ represents the vertical intercept or $y$ -intercept of the line as it is the value of $y$ when $x = 0$ . Also, there is an alternative method to find the intercepts of a line equation. Convert the given line equation into intercept form of a line i.e., $\dfrac{x}{a} + \dfrac{y}{b} = 1$ , where $a$ is the $x$ -intercept and $b$ is the $y$ -intercept.